题目内容
已知函数f(x)=x-x2+3lnx
(Ⅰ)求在P(1,0)处的切线方程;
(Ⅱ)证明f(x)≤2x-2.
(Ⅰ)求在P(1,0)处的切线方程;
(Ⅱ)证明f(x)≤2x-2.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数,得到f′(1),然后直接由直线方程的点斜式得切线方程;
(Ⅱ)构造函数g(x)=f(x)-2x+2,由导函数求其在(0,+∞)上的最大值,得到最大值为0,则结论得证.
(Ⅱ)构造函数g(x)=f(x)-2x+2,由导函数求其在(0,+∞)上的最大值,得到最大值为0,则结论得证.
解答:
(Ⅰ)解:∵f(x)=x-x2+3lnx (x>0),
∴f′(x)=1-2x+
,
则f′(1)=1-2×1+3=2,
∴曲线在P(1,0)处的切线方程为y-0=2(x-1),
即2x-y-2=0;
(Ⅱ)证明:令g(x)=f(x)-2x+2=x-x2+3lnx-2x+2=3lnx-x2-x+2 (x>0).
g′(x)=
-2x-1=
=
,
当x∈(0,1)时,g′(x)>0,g(x)为增函数;
当x∈(1,+∞)时,g′(x)<0,g(x)为减函数.
∴当x=1时,g(x)有极大值,也是(0,+∞)上的最大值,为3ln1-12-1+2=0.
∴g(x)=f(x)-2x+2≤0.
即f(x)≤2x-2.
∴f′(x)=1-2x+
| 3 |
| x |
则f′(1)=1-2×1+3=2,
∴曲线在P(1,0)处的切线方程为y-0=2(x-1),
即2x-y-2=0;
(Ⅱ)证明:令g(x)=f(x)-2x+2=x-x2+3lnx-2x+2=3lnx-x2-x+2 (x>0).
g′(x)=
| 3 |
| x |
| 3-x-2x2 |
| x |
| (3+2x)(1-x) |
| x |
当x∈(0,1)时,g′(x)>0,g(x)为增函数;
当x∈(1,+∞)时,g′(x)<0,g(x)为减函数.
∴当x=1时,g(x)有极大值,也是(0,+∞)上的最大值,为3ln1-12-1+2=0.
∴g(x)=f(x)-2x+2≤0.
即f(x)≤2x-2.
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了利用构造函数法比较两个函数式的大小,方法是利用导数求差函数的最值,是中档题.

练习册系列答案
相关题目
在区间[-1,4]内任取一个数x,则2x-x2≥
的概率是( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
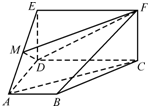 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=