题目内容
2.在各项均为正数的等比数列{an}中,a2,a4+2,a5成等差数列,a1=2,Sn是数列{an}的前n项的和,则S10-S4=2016.分析 设各项均为正数的等比数列{an}的公比为q>0,由a2,a4+2,a5成等差数列,a1=2,可得2(a4+2)=a2+a5,即2(2q3+2)=2q+2q4,解得q.再利用去韩国是即可得出.
解答 解:设各项均为正数的等比数列{an}的公比为q>0,
∵a2,a4+2,a5成等差数列,a1=2,
∴2(a4+2)=a2+a5,
∴2(2q3+2)=2q+2q4,
解得q=2.
∴S10-S4=$\frac{2({2}^{10}-1)}{2-1}-\frac{2({2}^{4}-1)}{2-1}$=2016.
故答案为:2016.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知一个路口的红绿灯,红灯的时间为35秒,黄灯的时间为5秒,绿灯的时间为60秒,老王开车上班要经过3个这样的路口,则老王遇见两次绿灯的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{13}{20}$ | C. | $\frac{54}{125}$ | D. | $\frac{27}{125}$ |
10.在等差数列{an}中,a2=3,a14=25,则a7+a9=( )
| A. | 22 | B. | 75 | C. | 28 | D. | 18 |
7.已知集合A={x|y=$\sqrt{x-2}$},B={x|x2-4<0},则A∪B=( )
| A. | ∅ | B. | (2,+∞) | C. | (-2,+∞) | D. | [0,2) |
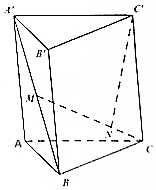 如图,若在三棱柱ABC-A′B′C′中,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AA′}$=$\overrightarrow{c}$,M是A′B的中点,点N在CM上,且CN:NM=1:2,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{CM}$、$\overrightarrow{C′N}$.
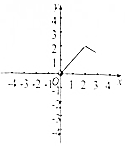
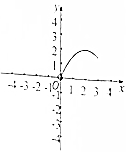
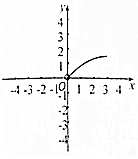
如图,若在三棱柱ABC-A′B′C′中,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AA′}$=$\overrightarrow{c}$,M是A′B的中点,点N在CM上,且CN:NM=1:2,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{CM}$、$\overrightarrow{C′N}$.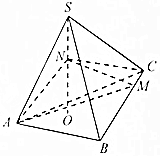 如图在三棱锥S-ABC中,CA=CB=3,∠ACB=30°,高SO=8,动点M、N分别在线段BC上SO上,且SN=2CM=2x,则下列四个图象中大致描绘了四面体AMCN的体积V与x变化关系(其中x∈(0,3])的是( )
如图在三棱锥S-ABC中,CA=CB=3,∠ACB=30°,高SO=8,动点M、N分别在线段BC上SO上,且SN=2CM=2x,则下列四个图象中大致描绘了四面体AMCN的体积V与x变化关系(其中x∈(0,3])的是( )