题目内容
10.在等差数列{an}中,a2=3,a14=25,则a7+a9=( )| A. | 22 | B. | 75 | C. | 28 | D. | 18 |
分析 利用等差数列的通项公式直接求解.
解答 解:在等差数列{an}中,
∵a2=3,a14=25,
∴a7+a9=a2+a14=3+25=28.
故选:C.
点评 本题考查等差数列中两项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
1.已知函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)在(0,$\frac{4π}{3}$]上单调递增,在($\frac{4π}{3}$,2π]上单调递减,当x∈[π,2π]时,不等式m-3≤f(x)≤m+3恒成立,则实数m的取值范围为( )
| A. | [$\frac{1}{2}$,1] | B. | (-∞,-2) | C. | [-$\frac{5}{2}$,4] | D. | [-2,$\frac{7}{2}$] |
5.函数f(x)=$\left\{\begin{array}{l}{-x-4,(x<0)}\\{{x}^{2}-4,(x>0)}\end{array}\right.$的零点为( )
| A. | -4或-2 | B. | -4或2 | C. | -2或4 | D. | -2或2 |
19.若动点A(x1,y1)、B(x2,y2)分别在直线l1:2x-y+11=0和l2:2x-y-1=0上移动,则AB的中点M所在的直线方程为( )
| A. | 2x+y-5=0 | B. | 2x+y+5=0 | C. | 2x-y-5=0 | D. | 2x-y+5=0 |
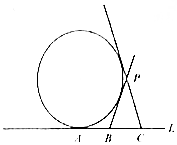 如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)
如图,A,B,C是直线l上的三点,AB=4,BC=4,过A作动圆与直线l相切,过B,C分别做圆的异于l的两切线,交于点P,则P的轨迹为椭圆.(填轨迹类型,不求方程)