题目内容
18．
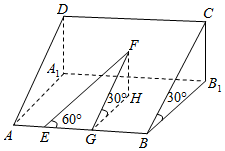如图所示，山坡的倾角为30°（就是坡面AC与地平面AB1所成的二面角是30°），山坡上有一条与斜坡底线AB成60°角的小路EF，如果某人从点E开始沿这条小路走了40m，问此人离开地平面的高度约为多少米（精确到1m）？
分析 据题意用式子表示出已知条件，通过勾股定理即可算出答案．
解答 解：如图所示：∠FEG=60°，∠FGH=30°，EF=40米，FH⊥平面AB1，
在Rt△FEG中，FG=FE•sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$（米），
在Rt△FGH中，FH=FG•sin30°=20$\sqrt{3}$×$\frac{1}{2}$=10$\sqrt{3}$≈17（米）．
点评 本题考查解三角形在实际问题中的应用，考查学生的理解能力及解决实际问题的能力，属中档题．
练习册系列答案
相关题目
8．集合A={x|-1≤x≤1}，B={x|x∈Z}，则A∩B=（ ）
| A． | （-1，1） | B． | {0，1} | C． | {-1，0，1} | D． | {1} |
6．
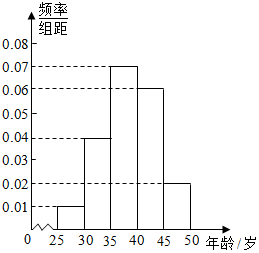某iphone手机专卖店对某市市民进行iphone手机认可度的调查，在已购买iPhone手机的1000名市民中随机抽取100名，按年龄（单位：岁）进行统计的频率分布表和频率分布直方图如下：
（1）求频数分布表中x，y的值；
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加iphone手机宣传活动，现从这20人中随机选取2人各赠送一部iphone6s手机，设这2名市民中年龄在[40，45）内的人数为X，求X的分布列及数学期望．
某iphone手机专卖店对某市市民进行iphone手机认可度的调查，在已购买iPhone手机的1000名市民中随机抽取100名，按年龄（单位：岁）进行统计的频率分布表和频率分布直方图如下：| 分组（岁） | 频数 |
| [25，30） | 5 |
| [30，35） | x |
| [35，40） | 35 |
| [40，45） | y |
| [45，50] | 10 |
| 合计 | 100 |
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加iphone手机宣传活动，现从这20人中随机选取2人各赠送一部iphone6s手机，设这2名市民中年龄在[40，45）内的人数为X，求X的分布列及数学期望．
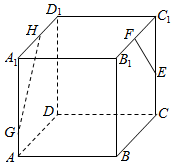如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别为边CC1、B1C1的中点，点G、H分别在AA1、D1A1上，且满足AA1=3AG，D1H=2HA1，则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$．
8．已知sinθ=$\frac{m-3}{m+5}$，cosθ=$\frac{4-2m}{m+5}$，其中$\frac{π}{2}$＜θ＜π，则tanθ=（ ）
| A． | -$\sqrt{2}$ | B． | -$\frac{12}{5}$ | C． | -2 | D． | -$\frac{5}{12}$ |