题目内容
设f(x)为定义在R上偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,0),斜率为1的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且过点(-1,1)的一段抛物线,试写出函数f(x)的表达式,并作出其图象.
考点:函数奇偶性的性质,函数的表示方法
专题:
分析:x≤-1时,用点斜式求得,x≥1时用偶函数求得,(-1<x<1时,用待定系数法求得.
解答:
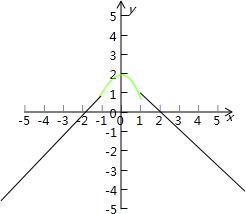 解:经过点(-2,0),斜率为1的射线:y=x+2 (x≤-1)
解:经过点(-2,0),斜率为1的射线:y=x+2 (x≤-1)
抛物线过(-1,1)和(0,2)
令y=ax2+c
代入,得y=-x2+2 (-1<x<1)
又函数在R上是偶函数
所以x≥1时,射线经过(2,0)且斜率为-1
即y=-x+2 (x≥1)
所以f(x)=
x<1
 解:经过点(-2,0),斜率为1的射线:y=x+2 (x≤-1)
解:经过点(-2,0),斜率为1的射线:y=x+2 (x≤-1)抛物线过(-1,1)和(0,2)
令y=ax2+c
代入,得y=-x2+2 (-1<x<1)
又函数在R上是偶函数
所以x≥1时,射线经过(2,0)且斜率为-1
即y=-x+2 (x≥1)
所以f(x)=
|
点评:本题主要考查分段函数及函数的图象.

练习册系列答案
相关题目
 .对
.对 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项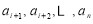 的最小值记为
的最小值记为 ,
, .
. 为
为 ,写出
,写出 ,
, ,
, 的值;
的值; (
( )是公比大于
)是公比大于 的等比数列,且
的等比数列,且 .证明:
.证明: 是等比数列;
是等比数列; 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列.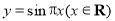 的部分图象如图所示,设
的部分图象如图所示,设 为坐标原点,
为坐标原点,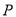 是图象的最高点,
是图象的最高点,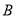 是图象与
是图象与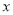 轴的交点,则
轴的交点,则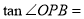 __________.
__________.


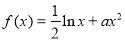
 .
.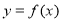 在点
在点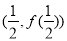 处的切线
处的切线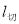 与直线
与直线 :
: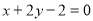 垂直,求
垂直,求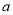 的值;
的值;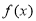 的单调性;若存在极值点
的单调性;若存在极值点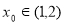 ,求实数
,求实数 的取值范围.
的取值范围.