题目内容
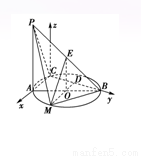
(本题满分12分)如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.

(1)求证:平面MOE∥平面PAC;
(2)求证:平面PAC⊥平面PCB;
(3)设二面角M-BP-C的大小为θ,求cosθ的值.
(1)见解析;(2)见解析;(3)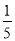
【解析】
试题分析:(1)因为点E为线段PB的中点,点O为线段AB的中点,
所以OE∥PA.
因为PA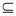 平面PAC,OE?平面PAC,
平面PAC,OE?平面PAC,
所以OE∥平面PAC.
因为OM∥AC,
又AC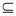 平面PAC,OM?平面PAC,
平面PAC,OM?平面PAC,
所以OM∥平面PAC.
因为OE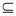 平面MOE,OM
平面MOE,OM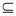 平面MOE,OE∩OM=O,
平面MOE,OE∩OM=O,
所以平面MOE∥平面PAC. 4分
(2)因为点C在以AB为直径的⊙O上,
所以∠ACB=90°,即BC⊥AC.
因为PA⊥平面ABC,BC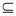 平面ABC,
平面ABC,
所以PA⊥BC.
因为AC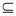 平面PAC,PA
平面PAC,PA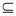 平面PAC,PA∩AC=A,
平面PAC,PA∩AC=A,
所以BC⊥平面PAC.
因为BC 平面PBC,所以平面PAC⊥平面PBC. 9分
平面PBC,所以平面PAC⊥平面PBC. 9分
(3)如图,以C为原点,CA所在的直线为x轴,CB所在的直线为y轴,建立空间直角坐标系C-xyz.
因为∠CBA=30°,PA=AB=2,
所以CB=2cos30°=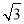 ,AC=1.
,AC=1.
延长MO交CB于点D.
因为OM∥AC,
所以MD⊥CB,MD=1+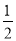 =
=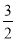 ,CD=
,CD=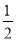 CB=
CB=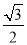 .
.
所以P(1,0,2),C(0,0,0),B(0,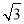 ,0),M(
,0),M(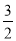 ,
,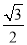 ,0).
,0).
所以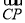 =(1,0,2),
=(1,0,2),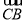 =(0,
=(0,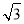 ,0).
,0).
设平面PCB的法向量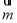 =(x,y,z).
=(x,y,z).
因为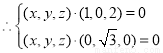 即
即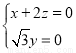
令z=1,则x=-2,y=0.
所以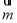 =(-2,0,1).
=(-2,0,1).
同理可求平面PMB的一个法向量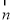 =(1,
=(1,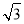 ,1).
,1).
所以cos〈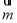 ,
,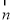 〉=
〉=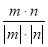 =-
=- .所以cosθ=
.所以cosθ=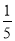 . 12分
. 12分
考点:本题考查面面平行的判定,面面垂直的判定,二面角的求法

 与函数
与函数
 的图象恰有三个公共点,则实数
的图象恰有三个公共点,则实数 的取值范围是( )
的取值范围是( )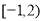 (B)
(B) (C)
(C)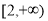 (D)
(D)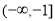
 ,
, ,则
,则 等于( )
等于( ) (B)
(B) (C)
(C) (D)
(D)
 的二项展开式中,
的二项展开式中, 的系数为
的系数为 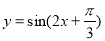 在区间
在区间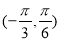 内单调递增
内单调递增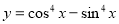 的最小正周期为
的最小正周期为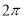
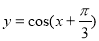 的图像是关于点
的图像是关于点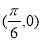 成中心对称的图形
成中心对称的图形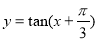 的图像是关于直线
的图像是关于直线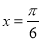 成轴对称的图形
成轴对称的图形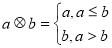 ,令
,令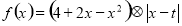 (
(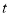 为常数),且
为常数),且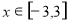 ,则使函数
,则使函数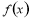 最大值为4的
最大值为4的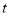 值是( )
值是( ) 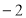 或
或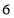 B.
B.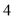 或
或 C.
C.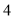 D.
D.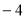 或
或 的所有数按照从大到小的原则写成如下数表:
的所有数按照从大到小的原则写成如下数表: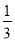


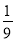
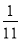






 行有
行有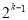 个数,第
个数,第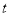 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则