题目内容
将下列函数转化为Asin(ωx+φ)+B的形式,
(1)f(x)=cosx(sinx-cosx)+1
(2)f(x)=2
sinxcosx-2sin2x.
(1)f(x)=cosx(sinx-cosx)+1
(2)f(x)=2
| 3 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(1)运用二倍角的正弦和余弦公式以及两角差的正弦公式,化简即可得到;
(2)运用二倍角的正弦和余弦公式以及两角和的正弦公式,化简即可得到.
(2)运用二倍角的正弦和余弦公式以及两角和的正弦公式,化简即可得到.
解答:
解:(1)f(x)=cosx(sinx-cosx)+1
=cosxsinx-cos2x-1=
sin2x-
(1+cos2x)-1
=
(
sin2x-
cos2x)-
=
sin(2x-
)-
;
(2)f(x)=2
sinxcosx-2sin2x
=
sin2x-(1-cos2x)
=2(
sin2x+
cos2x)-1
=2sin(2x+
)-1.
=cosxsinx-cos2x-1=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 3 |
| 2 |
(2)f(x)=2
| 3 |
=
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2sin(2x+
| π |
| 6 |
点评:本题考查三角函数的化简,主要考查二倍角的正弦和余弦公式以及两角和差的正弦公式的运用,属于基础题.

练习册系列答案
相关题目
点P为底边长为2
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
•
取值范围是( )
| 3 |
| PM |
| PN |
| A、[0,2] |
| B、[0,3] |
| C、[0,4] |
| D、[-2,2] |
下列函数为偶函数的是( )
| A、f(x)=x2 |
| B、f(x)=lnx |
| C、f(x)=ex |
| D、f(x)=sinx |
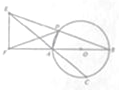 如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F.
如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F. 在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=
在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=