题目内容
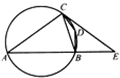
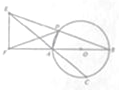如图所示，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA并交BA的延长线于点F．（Ⅰ）求证：∠EFD=∠DAE；
（Ⅱ）求证：AB2=BE•BD-AE•AC．
考点：与圆有关的比例线段
专题：直线与圆
分析：（Ⅰ）连结AD，得∠ADB=90°，从而∠ADE=90°，再由∠AFE=90°，得A、D、E、F四点共圆，从而能证明∠EFD=∠DAE．
（2）由A、D、E、F四点共圆，得BD•BE=BA•BF，再由△ABC～△AEF，得AB•AF=AE•AC，由此能证明AB2=BD•BE-AE•AC．
（2）由A、D、E、F四点共圆，得BD•BE=BA•BF，再由△ABC～△AEF，得AB•AF=AE•AC，由此能证明AB2=BD•BE-AE•AC．
解答：
证明：（Ⅰ）连结AD，∵AB是圆的直径，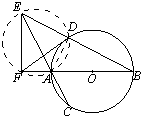
∴∠ADB=90°，∴∠ADE=90°，
又∵∠AFE=90°，∴A、D、E、F四点共圆，
∴∠EFD=∠DAE．
（2）由A、D、E、F四点共圆，得BD•BE=BA•BF，
又∵△ABC～△AEF，∴
=
，
∴AB•AF=AE•AC，
∴BE•BD-AE•AC=BA•BF-AB•AF=AB•（BF-AF）=AB2，
∴AB2=BD•BE-AE•AC．
∴∠ADB=90°，∴∠ADE=90°，
又∵∠AFE=90°，∴A、D、E、F四点共圆，
∴∠EFD=∠DAE．
（2）由A、D、E、F四点共圆，得BD•BE=BA•BF，
又∵△ABC～△AEF，∴
| AB |
| AE |
| AC |
| AF |
∴AB•AF=AE•AC，
∴BE•BD-AE•AC=BA•BF-AB•AF=AB•（BF-AF）=AB2，
∴AB2=BD•BE-AE•AC．
点评：本题考查两角相等的证明，考查AB2=BE•BD-AE•AC的证明，是中档题，解题时要认真审题，注意四点共圆的性质的合理运用．
练习册系列答案
相关题目
设集合U={1，2，3，4，5，6，7}，M={2，4，7}，则∁UM=（ ）
| A、U |
| B、{1，2，6} |
| C、{1，3，5，6} |
| D、{1，3，5} |
如图，四边形么BDC内接于圆，BD=CD，过C点的圆的切线与AB的延长线交于E点．已知某几何体的三视图如图所示，则该几何体的体积是（ ）
A、8
| ||||
B、
| ||||
C、
| ||||
D、16
|
已知某个几何体的三视图如图，则这个几何体的表面积为（ ）
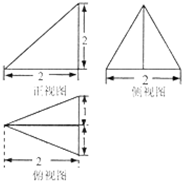
A、4+
| ||
B、4+2
| ||
| C、6 | ||
| D、8 |