题目内容
某同学在研究函数f(x)=
(x∈R) 时,分别给出下面几个结论:
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x1≠x2,则一定有f (x1)≠f (x2);
④函数g(x)=f(x)-x在R上有三个零点.
其中正确结论的序号是( )
| x |
| 1+|x| |
①等式f(-x)+f(x)=0在x∈R时恒成立;
②函数 f (x) 的值域为 (-1,1);
③若x1≠x2,则一定有f (x1)≠f (x2);
④函数g(x)=f(x)-x在R上有三个零点.
其中正确结论的序号是( )
| A、①② | B、①②③ |
| C、①③④ | D、①②③④ |
考点:函数的值域
专题:函数的性质及应用
分析:可以先研究函数的奇偶性,然后做出函数的图象,据此求解.
解答:
解:易知函数的定义域为R,且f(-x)=-f(x),故函数为奇函数.故①正确;
当x>0时,f(x)=
=
,该函数在(0,+∞)上递增,且x→0时,f(x)→0;当x→+∞时,f(x)→1.
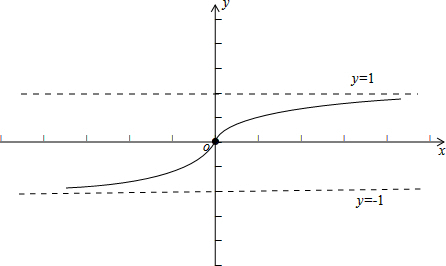
结合奇偶性,作出f(x)的图象如下:
易知函数的值域是(-1,1),故②正确;
结合函数为定义域内的增函数,所以③正确;
又x≥0时,g(x)=f(x)-x=
-x=
,
令f(x)-x=0得x=0,故此时g(x)只有一个零点0,g(x)显然是奇函数,故该函数只有一个零点,所以④错误.
故正确的命题是①②③.
故选B
当x>0时,f(x)=
| x |
| 1+x |
| 1 | ||
1+
|
结合奇偶性,作出f(x)的图象如下:
易知函数的值域是(-1,1),故②正确;
结合函数为定义域内的增函数,所以③正确;
又x≥0时,g(x)=f(x)-x=
| x |
| 1+x |
| -x2 |
| 1+x |
令f(x)-x=0得x=0,故此时g(x)只有一个零点0,g(x)显然是奇函数,故该函数只有一个零点,所以④错误.
故正确的命题是①②③.
故选B

点评:本题考查了函数的性质.一般先研究定义域,然后判断函数的奇偶性、单调性等性质作为突破口,有一些要结合函数的图象加以分析,注意数形结合的思想的应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知过抛物线C:x2=2py(p>0)的焦点F的直线m交抛物线于点M、N,|MF|=2,|NF|=3,则抛物线C的方程为( )
| A、x2=8y | ||
| B、x2=2y | ||
| C、x2=4y | ||
D、x2=2
|
若0<a<b,a+b=1,则a,
,2ab,a2+b2中最大的数为( )
| 1 |
| 2 |
| A、a | ||
B、
| ||
| C、2ab | ||
| D、a2+b2 |
