题目内容
(1)计算:(0.25)0-(
)-0.75+
+
+ln
+22+lo
;
(2)已知14a=6,14b=7,用a,b表示log4256.
| 1 |
| 16 |
| 4 | (1-
| ||
6-4
|
| e |
| g | 3 2 |
(2)已知14a=6,14b=7,用a,b表示log4256.
考点:对数的运算性质,有理数指数幂的化简求值
专题:函数的性质及应用
分析:(1)利用指数与对数的运算法则即可得出.
(2)利用对数的换底公式、运算法则即可得出.
(2)利用对数的换底公式、运算法则即可得出.
解答:
解:(1)原式=1-(2-4)-
+
-1+2-
+
+22×2log23
=1-8+1+
+12
=
.
(2)∵14a=6,14b=7,∴log146=a,log147=b.
∴log4256=
=
=
=
=
.
| 3 |
| 4 |
| 2 |
| 2 |
| 1 |
| 2 |
=1-8+1+
| 1 |
| 2 |
=
| 13 |
| 2 |
(2)∵14a=6,14b=7,∴log146=a,log147=b.
∴log4256=
| log144+log1414 |
| log146+log147 |
| 1+2log142 |
| a+b |
1+2log14
| ||
| a+b |
| 3-2log147 |
| a+b |
| 3-2b |
| a+b |
点评:本题考查了指数与对数的运算法则、对数的换底公式,属于基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
在用二分法求方程x3-2x-1=0的一个近似解时,现在已经将一根锁定在区间(1,2)内,则下一步可断定该根所在的区间为( )
| A、(1.4,2) | ||
| B、(1.1,4 ) | ||
C、(1,
| ||
D、(
|
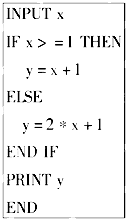 读程序,完成下列题目:程序如图:
读程序,完成下列题目:程序如图: