题目内容
在用二分法求方程x3-2x-1=0的一个近似解时,现在已经将一根锁定在区间(1,2)内,则下一步可断定该根所在的区间为( )
| A、(1.4,2) | ||
| B、(1.1,4 ) | ||
C、(1,
| ||
D、(
|
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:由题意构造函数f(x)=x3-2x-1,求方程x3-2x-1=0的一个近似解,就是求函数在某个区间内有零点,因此把x=1.2,
代入函数解析式,分析函数值的符号是否异号即可.
| 3 |
| 2 |
解答:
解:令f(x)=x3-2x-1,
则f(1)=-2<0,f(2)=3>0,f(
)=-
<0
由f(
)•f(2)<0知根所在区间为(
,2)
故选D.
则f(1)=-2<0,f(2)=3>0,f(
| 3 |
| 2 |
| 5 |
| 8 |
由f(
| 3 |
| 2 |
| 3 |
| 2 |
故选D.
点评:此题是个基础题.考查二分法求方程的近似解,以及方程的根与函数的零点之间的关系,体现了转化的思想,同时也考查了学生分析解决问题的能力.

练习册系列答案
相关题目
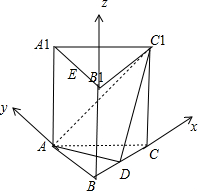 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.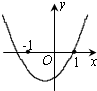 已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )
已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )