题目内容
定义f(x,y)=(y2,2y-x),若f(m,n)=(1,2),则(m,n)= .
考点:函数的值
专题:函数的性质及应用
分析:由已知得y2=1,从而2y-x=2,由此能求出(m,n)=(-4,-1)或(0,1).
解答:
解:∵定义f(x,y)=(y2,2y-x),
∴f(m,n)=(1,2),
∵y2=1,
∴2y-x=2,
解得y=-1或y=1,
∴x=-4或x=0,
故(m,n)=(-4,-1)或(0,1).
故答案为:(-4,-1)或(0,1).
∴f(m,n)=(1,2),
∵y2=1,
∴2y-x=2,
解得y=-1或y=1,
∴x=-4或x=0,
故(m,n)=(-4,-1)或(0,1).
故答案为:(-4,-1)或(0,1).
点评:本题考查函数值的求法,是基础题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)是偶函数,且在(-∞,0]上是减函数,若f(22x2-x-1)≥f(-4),则x的取值范围是( )
A、(-∞,-1]∪[
| ||
B、(-∞,-
| ||
| C、[-1,2] | ||
| D、[-2,1] |
函数y=sin2x的图象经过适当变换可以得到y=cos2x的图象,则这种变换可以是( )
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向左平移
| ||
D、沿x轴向右平移
|
设a=50.8,b=0.67,c=log0.74,则a,b,c的大小关系是( )
| A、a<c<b |
| B、c<a<b |
| C、b<a<c |
| D、c<b<a |
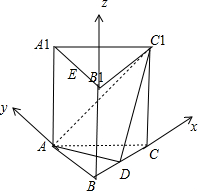 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.