题目内容
观察下列等式:1=12,1+2+1=22,1+2+3+2+1=32,…由此猜想第n个等式为 .
考点:归纳推理
专题:推理和证明
分析:根据已知观察,可知:等号左边是从1开始,连续整数加到n再倒序加到1,等号右边是n的平方.
解答:
解:由已知中等式:
1=12,
1+2+1=22,
1+2+3+2+1=32,
…
归纳可得:等号左边是从1开始,连续整数加到n再倒序加到1,等号右边是n的平方,
故第n个等式为1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2,
故答案为:1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2
1=12,
1+2+1=22,
1+2+3+2+1=32,
…
归纳可得:等号左边是从1开始,连续整数加到n再倒序加到1,等号右边是n的平方,
故第n个等式为1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2,
故答案为:1+2+3+…+(n-1)+n+(n-1)+…+3+2+1=n2
点评:本题为规律探究题,通过数表,寻找数字间的规律并运用这一规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
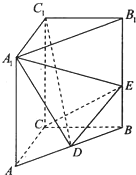 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB= 如图,AP是⊙O的切线,A为切点,AE=3,EC=4,BE=6,PE=6,则AP=
如图,AP是⊙O的切线,A为切点,AE=3,EC=4,BE=6,PE=6,则AP=