题目内容
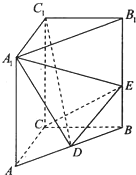 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,E为BB1上一点,且| BE |
| EB1 |
(Ⅰ)当λ=
| 2 |
| 7 |
(Ⅱ)若直线CE与平面A1DE所成的角为30°,求λ的值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)建立空间直角坐标系,证明
•
=0,
•
=0,即可证明CE⊥平面A1C1D;
(Ⅱ)求出平面A1DE的一个法向量,直线CE的向量,根据直线CE与平面A1DE所成的角为30°,利用向量的夹角公式,即可求λ的值.
| CE |
| C1A1 |
| CE |
| C1D |
(Ⅱ)求出平面A1DE的一个法向量,直线CE的向量,根据直线CE与平面A1DE所成的角为30°,利用向量的夹角公式,即可求λ的值.
解答:
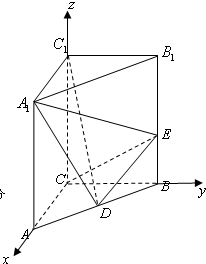 (Ⅰ)证明:建立空间直角坐标系如图所示,则C(0,0,0),A(2,0,0),B(0,2,0),A1(2,0,3),B1(0,2,3),C1(0,0,3),D(1,1,0),
(Ⅰ)证明:建立空间直角坐标系如图所示,则C(0,0,0),A(2,0,0),B(0,2,0),A1(2,0,3),B1(0,2,3),C1(0,0,3),D(1,1,0),
∵λ=
,∴E(0,2,
),
∴
=(0,2,
)…(3分)
又
=(2,0,0),
=(1,1,-3)
∴
•
=0,
•
=0,
∴CE⊥平面A1C1D;…(6分)
(Ⅱ)解:由题知E(0,2,
),
=(0,2,
),
=(-1,1,-3),
=(-1,1,
),
∴平面A1DE的一个法向量为
=(3+
,3+
,0)…(9分)
∴|
|=
即
=
解得λ=2.…(13分)
 (Ⅰ)证明:建立空间直角坐标系如图所示,则C(0,0,0),A(2,0,0),B(0,2,0),A1(2,0,3),B1(0,2,3),C1(0,0,3),D(1,1,0),
(Ⅰ)证明:建立空间直角坐标系如图所示,则C(0,0,0),A(2,0,0),B(0,2,0),A1(2,0,3),B1(0,2,3),C1(0,0,3),D(1,1,0),∵λ=
| 2 |
| 7 |
| 2 |
| 3 |
∴
| CE |
| 2 |
| 3 |
又
| C1A1 |
| C1D |
∴
| CE |
| C1A1 |
| CE |
| C1D |
∴CE⊥平面A1C1D;…(6分)
(Ⅱ)解:由题知E(0,2,
| 3λ |
| 1+λ |
| CE |
| 3λ |
| 1+λ |
| A1D |
| DE |
| 3λ |
| 1+λ |
∴平面A1DE的一个法向量为
| n |
| 3λ |
| 1+λ |
| 3λ |
| 1+λ |
∴|
| ||||
|
|
| 1 |
| 2 |
即
2(3+
| ||||||||
|
| 1 |
| 2 |
点评:本题考查线面垂直,考查直线与平面所成的角,考查向量知识的运用,确定向量的坐标是关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).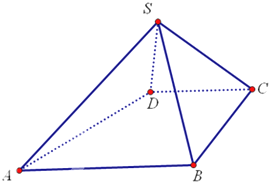 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.