题目内容
若二次函数f(x)=x2-ax+2a-1仅存在整数零点,则实数a的集合为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:若二次函数f(x)=x2-ax+2a-1仅存在整数零点,则x2-ax+2a-1=0仅有整数根,则x=
是整数.进而由韦达定理可得a是整数,分析讨论后可得实数a的集合.
a±
| ||
| 2 |
解答:
解:若二次函数f(x)=x2-ax+2a-1仅存在整数零点,
则x2-ax+2a-1=0仅有整数根,
即x=
是整数.
∴设a2-8a+4=k2,
则a=4±
,
∵x1+x2=a,a是整数,故
也是整数,
即k2+12是个完全平方数,设k2+12=n2,
则n2-k2=12,
∴(n-k)(n+k)=12,
又由(n-k),(n+k)的奇偶性相同,
故n-k,n+k的值只能为2,6,或-2,-6,
∵解得n=4,n=-4,
∴a=0或a=8,
代入验证后,a=0或a=8都符合题意.
故实数a的集合为{0,8},
故答案为:{0,8}
则x2-ax+2a-1=0仅有整数根,
即x=
a±
| ||
| 2 |
∴设a2-8a+4=k2,
则a=4±
| k2+12 |
∵x1+x2=a,a是整数,故
| k2+12 |
即k2+12是个完全平方数,设k2+12=n2,
则n2-k2=12,
∴(n-k)(n+k)=12,
又由(n-k),(n+k)的奇偶性相同,
故n-k,n+k的值只能为2,6,或-2,-6,
∵解得n=4,n=-4,
∴a=0或a=8,
代入验证后,a=0或a=8都符合题意.
故实数a的集合为{0,8},
故答案为:{0,8}
点评:本题考查的知识点是二次函数的性质,方程的根,分类讨论思想,转化难度比较大,属于难题.

练习册系列答案
相关题目
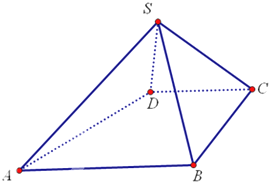 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1. 已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.
已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD. 底面直径为10的圆柱被与底面成60°的平面所截,截口是一个椭圆,该椭圆的长轴长
底面直径为10的圆柱被与底面成60°的平面所截,截口是一个椭圆,该椭圆的长轴长