题目内容
13.设a=$\frac{1}{2}$cos8°-$\frac{\sqrt{3}}{2}$sin8°,b=$\frac{2tan14°}{1-ta{n}^{2}14°}$,c=$\sqrt{\frac{1-cos48°}{2}}$;则有( )| A. | a<c<b | B. | a<b<c | C. | c<b<a | D. | b<c<a |
分析 利用辅助角公式可得a=sin22°,由二倍角的正切公式,可得b=tan26°,由半角公式,可得c=sin26°,再结合正弦函数的单调性和同角三角函数关系,即可得到a,b,c的大小关系.
解答 解:a=$\frac{1}{2}$cos8°-$\frac{\sqrt{3}}{2}$sin8°=sin30°cos8°-cos30°sin8°=sin22°.
b=$\frac{2tan14°}{1-ta{n}^{2}14°}$=tan26°,
c=$\sqrt{\frac{1-cos48°}{2}}$=sin26°
∵sin22°<sin26°<tan26°
∴a<c<b.
故选:A.
点评 本题考查的知识点是三角函数的恒等变换及化简求值,其中根据两角和余弦公式、诱导公式、二倍角的正切公式、半角公式,求出a,b,c的值,是解答本题的关键.

练习册系列答案
相关题目
1.复数$\frac{2}{1-i}$=( )
| A. | $\sqrt{2}$+$\sqrt{2}$i | B. | $\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$i | C. | 1-i | D. | 1+i |
18.已知集合A={x|x2-16<0},B={-4,-2,0,1},则( )
| A. | B⊆A | B. | A∩B=∅ | C. | A∩B={0,1} | D. | A∩B={-2,0,1} |
2.若在△ABC中,sinA:sinB:sinC=3:5:6,则sinB等于( )
| A. | $\frac{{2\sqrt{14}}}{9}$ | B. | $\frac{{\sqrt{14}}}{9}$ | C. | $\frac{{\sqrt{11}}}{5}$ | D. | $\frac{{2\sqrt{11}}}{5}$ |
3.2016年上半年数据显示,某市空气质量在其所在省中排名倒数第三,PM10(可吸入颗粒物)和PM2.5(细颗粒物)分别排在倒数第一和倒数第四,这引起有关部门高度重视,该市采取一系列“组合拳”治理大气污染,计划到2016年底,全年优、良天数达到190天.下表是2016年9月1日到9月15日该市的空气质量指数(AQI),其中空气质量指数划分为0~50,51~100,101~150,151~200,201~300和大于300六档,对应空气质量依次为优、良、轻度污染、中度污染、重度污染、严重污染.
(1)指出这15天中PM2.5的最大值及PM10的最大值;
(2)从这15天中连续取2天,求这2天空气质量均为优、良的概率;
(3)已知2016年前8个月(每个月按30天计算)该市空气质量为优、良的天数约占55%,用9月份这15天空气质量优、良的频率作为2016年后4个月空气质量优、良的概率(不考虑其他因素),估计该市到2016年底,能否完成全年优、良天数达到190天的目标.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
| AQI指数 | 72 | 74 | 115 | 192 | 138 | 123 | 74 | 80 | 105 | 73 | 91 | 90 | 77 | 109 | 124 |
| PM2.5 | 36 | 29 | 76 | 112 | 89 | 85 | 40 | 32 | 59 | 35 | 45 | 59 | 53 | 79 | 89 |
| PM10 | 76 | 86 | 148 | 199 | 158 | 147 | 70 | 83 | 121 | 75 | 96 | 90 | 63 | 113 | 140 |
(2)从这15天中连续取2天,求这2天空气质量均为优、良的概率;
(3)已知2016年前8个月(每个月按30天计算)该市空气质量为优、良的天数约占55%,用9月份这15天空气质量优、良的频率作为2016年后4个月空气质量优、良的概率(不考虑其他因素),估计该市到2016年底,能否完成全年优、良天数达到190天的目标.
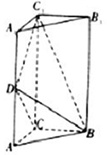 如图,直三棱柱ABC-A1B1C1中,$AC=BC=AD={A_1}D=1,BD=\sqrt{3}$.
如图,直三棱柱ABC-A1B1C1中,$AC=BC=AD={A_1}D=1,BD=\sqrt{3}$.