题目内容
已知实数a,b,c满足a>c-2且3a+3b<31+c,则
的取值范围是 .
| 3a-3b |
| 3c |
考点:不等式的基本性质,有理数指数幂的运算性质
专题:不等式的解法及应用
分析:先由条件利用不等式的基本性质求得3a-c-3b-c<3 ①,再求得3a-c-3b-c>-
②,综合可得3a-c-3b-c 的范围,即为所求.
| 25 |
| 9 |
解答:
解:∵实数a,b,c满足a>c-2且3a+3b<31+c,
∴3a-c>3-2=
,3a-c+3b-c<3.
再由3b-c>0,可得3a-c-3b-c<3 ①.
再由3b-c<3-3a-c<3-
=
,可得-3b-c>-
,∴3a-c-3b-c>
-
=-
②,
由①②可得-
<3a-c-3b-c<3,即
的取值范围为(-
,3),
故答案为:(-
,3).
∴3a-c>3-2=
| 1 |
| 9 |
再由3b-c>0,可得3a-c-3b-c<3 ①.
再由3b-c<3-3a-c<3-
| 1 |
| 9 |
| 26 |
| 9 |
| 26 |
| 9 |
| 1 |
| 9 |
| 26 |
| 9 |
| 25 |
| 9 |
由①②可得-
| 25 |
| 9 |
| 3a-3b |
| 3c |
| 25 |
| 9 |
故答案为:(-
| 25 |
| 9 |
点评:本题主要考查不等式的基本性质的应用,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 已知函数f(x)=2cos2(
已知函数f(x)=2cos2(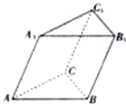 如图所示,在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2
如图所示,在三棱柱ABC-A1B1C1中,AB=AC=AA1=2,BC=2