Question

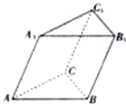如图所示，在三棱柱ABC-A₁B₁C₁中，AB=AC=AA₁=2，BC=2

2

，且∠A₁AB=∠A₁AC=60°，则该三棱柱的体积是

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：综合题,空间位置关系与距离

分析：因为AB=AC=2，BC=2

2

，所以∠CAB=45°．由于∠A₁AB=∠A₁AC=60°，所以点A₁在底面内的投影点O必定在底部三角形ABC的∠BAC的角平分线上，进而可以求得线面角A₁AO，再在直角三角形A₁AO中解出该棱柱的高即可求其体积．

解答： 解：∵AB=AC=2，BC=2

2

，∴∠CAB=45°．
∵∠A₁AB=∠A₁AC=60°，
∴点A₁在底面内的投影点O必定在底部三角形ABC的∠BAC的角平分线上，
由公式cos∠A₁AB=cos∠A₁AO×cos∠OAB?cos60°=cos∠A₁AO×cos45°
∴cos∠A₁AO=

2

2

∴在直角三角形A₁A0中：A₁O=

2

∴该柱体的体积为：

1

2

•2•2•

2

=2

2

．
故答案为：2

2

．

点评：此题考查了线面角的定理，柱体的体积公式，公式cos∠A₁AB=cos∠A₁AO×cos∠OAB，属于中档题．