题目内容
(1)证明:f(x)是R上的偶函数.
(2)若关于x的不等式mf(x)≤e-x +m-1在(0,+∞)上恒成立,求实数m的取值范围.
(3)已知正数a满足:存在x0∈[1,+∞),使得f (x0)<a(-x
(x0)<a(-x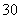 +3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
+3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
[解析]
(1)证明:因为对任意 x∈R,都有f(-x)=e-x+e -(-x)=e-x+ex=f(x),
所以f(x)是R上的偶函数.
(2)由条件知 m(ex+e-x-1)≤e-x-1在(0,+∞)上恒成立.
令 t=ex(x>0),则 t>1,所以 m≤ 对任意 t>1成立.
对任意 t>1成立.
因为 =3, 所以 -
=3, 所以 - ≥-
≥- ,
,
当且仅当 t=2, 即x = ln 2时等号成立.
因此实数 m 的取值范围是 .
.
(3)令函数 g(x)=ex+ - a(-x3+3x),则g′ (x) =ex-
- a(-x3+3x),则g′ (x) =ex- +3a(x2-1).
+3a(x2-1).
当 x≥1时,ex- >0,x2-1≥0.又a>0,故 g′(x)>0,所以g(x)是[1,+∞)上的单调递增函数, 因此g(x)在[1,+∞)上的最小值是 g(1)= e+e-1-2a.
>0,x2-1≥0.又a>0,故 g′(x)>0,所以g(x)是[1,+∞)上的单调递增函数, 因此g(x)在[1,+∞)上的最小值是 g(1)= e+e-1-2a.
由于存在x0∈[1,+∞),使ex0+e-x0-a(-x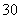 + 3x0 )<0 成立, 当且仅当最小值g(1)<0,
+ 3x0 )<0 成立, 当且仅当最小值g(1)<0,
故 e+e-1-2a<0, 即 a> .
.
令函数h(x) = x -(e-1)ln x-1,则 h′(x)=1- . 令 h′(x)=0, 得x=e-1.
. 令 h′(x)=0, 得x=e-1.
当x∈(0,e-1)时,h′(x)<0,故h(x)是(0,e-1)上的单调递减函数;
当x∈(e-1,+∞)时,h′(x)>0,故h(x)是(e-1,+∞)上的单调递增函数.
所以h(x)在(0,+∞)上的最小值是h(e-1).
注意到h(1)=h(e)=0,所以当x∈(1,e-1)⊆(0,e-1)时,h(e-1)≤h(x)<h(1)=0;
当x∈(e-1,e)⊆(e-1,+∞)时,
h(x)<h(e)=0.
所以h(x)<0对任意的x∈(1,e)成立.
故①当a∈ ⊆(1,e)时, h(a)<0,
⊆(1,e)时, h(a)<0,
即a-1<(e-1)ln a,从而ea-1<ae-1;
②当a=e时,ea-1=ae-1;
③当a∈(e,+∞)⊆(e-1,+∞)时,h(a)>h(e)=0,即a-1>(e-1)ln a,故ea-1>ae-1.
综上所述,当a∈ 时,ea-1<ae-1;当a=e时,ea-1=ae-1;
时,ea-1<ae-1;当a=e时,ea-1=ae-1;
当a∈(e,+∞)时,ea-1>ae-1.

 上总存在两个点到原点的距离为1,则实数
上总存在两个点到原点的距离为1,则实数 的取值范围____________.
的取值范围____________. 个小朋友分糖果.她发现糖果盒中原有糖果数为
个小朋友分糖果.她发现糖果盒中原有糖果数为 ,就先从别处抓2块糖加入盒中,然后把盒内糖果的
,就先从别处抓2块糖加入盒中,然后把盒内糖果的 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的 分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的 分给第
分给第 个小朋友.如果设分给第
个小朋友.如果设分给第 个小朋友后(未加入2块糖果前)盒内剩下的糖果数为
个小朋友后(未加入2块糖果前)盒内剩下的糖果数为 .
. ,
, 时,分别求
时,分别求 ;
; 表示
表示 ,求数列
,求数列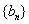 的通项公式;
的通项公式;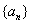
 成等差数列,如果存在,请求出所有的
成等差数列,如果存在,请求出所有的 和
和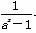 +
+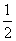 )x3(a>0且a≠1).
)x3(a>0且a≠1). ,其中
,其中 的单位是米,
的单位是米, 的单位是秒,那么物体在
的单位是秒,那么物体在 时的瞬时速度为 米/秒.
时的瞬时速度为 米/秒.
 在(1,+∞)上是减函数,则
在(1,+∞)上是减函数,则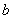 的取值范围是
的取值范围是  的图像在点
的图像在点 处的切线方程是
处的切线方程是 ,那么
,那么 .
.  中,点
中,点 .则以线段
.则以线段
 为邻边的平行四边形两条对角线的长分别为 .
为邻边的平行四边形两条对角线的长分别为 .