题目内容
一位幼儿园老师给班上 个小朋友分糖果.她发现糖果盒中原有糖果数为
个小朋友分糖果.她发现糖果盒中原有糖果数为 ,就先从别处抓2块糖加入盒中,然后把盒内糖果的
,就先从别处抓2块糖加入盒中,然后把盒内糖果的 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的 分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的 分给第
分给第 个小朋友.如果设分给第
个小朋友.如果设分给第 个小朋友后(未加入2块糖果前)盒内剩下的糖果数为
个小朋友后(未加入2块糖果前)盒内剩下的糖果数为 .
.
(1) 当 ,
, 时,分别求
时,分别求 ;
;
(2) 请用 表示
表示 ;令
;令 ,求数列
,求数列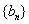 的通项公式;
的通项公式;
(3)是否存在正整数 和非负整数
和非负整数 ,使得数列
,使得数列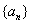
 成等差数列,如果存在,请求出所有的
成等差数列,如果存在,请求出所有的 和
和 ,如果不存在,请说明理由.
,如果不存在,请说明理由.
(1)当 ,
, 时,
时,  ,
,
 ,
,
(2)由题意知: ,
,
即 ,
, 
 ,
,


累加得 , 又
, 又 ,
,

(3)由 ,得
,得 ,
,
若存在正整数 和非负整数
和非负整数 ,使得数列
,使得数列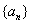
 成等差数列,
成等差数列,
则 , 即
, 即 ,
,
当 时,
时,  ,对任意正整数
,对任意正整数 ,有
,有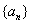
 成等差数列
成等差数列

练习册系列答案
相关题目
 中,
中, ,
, ,
, 分别是棱
分别是棱 上的点,
上的点, 为边
为边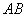 的中点,
的中点, ,则三角形
,则三角形 的面积为 .
的面积为 .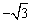 ,0),F(
,0),F(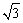 ,0),圆F:
,0),圆F: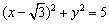 .动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为
.动点P满足PE+PF=4.以P为圆心,OP为半径的圆P与圆F的一个公共点为 Q.
Q.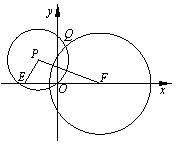
 ,则
,则 的最小值为_________.
的最小值为_________. 时,数列
时,数列 为正项等比数列,则当
为正项等比数列,则当 时,数列
时,数列 也是等比数列.
也是等比数列. |在区间[a,b]上的值域为[0,1],则b-a的最小值为________.
|在区间[a,b]上的值域为[0,1],则b-a的最小值为________.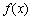 在
在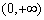 上为减函数,且
上为减函数,且 ,则不等式
,则不等式 的解集
的解集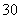 +3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
+3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.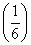 的值为______.
的值为______.