题目内容

在（x-2）5（
2
+y）4的展开式中，x3y2的系数为
 
．
考点：二项式系数的性质
专题：计算题,二项式定理
分析：利用二项展开式的通项公式，可得结论．
解答： 解：（x-2）5（
2
+y）4的展开式中，x3y2的系数为
C
2
5
•(-2)2•
C
2
4
•(
2
)2=480．
故答案为：480．
点评：二项展开式的通项公式是解决二项展开式的特定项问题的工具．
练习册系列答案
相关题目
集合A={α|α=
kπ
6
，k∈Z}，B={β|β=
nπ
3
+
π
6
，n∈Z}的关系是（　　）
A、A?BB、A?B
C、A⊆BD、A=B
已知函数f（x）=
|log5(1-x)|(x＜1)
-(x-2)2+2(x≥1)
，则关于x的方程f（|x|）=a的实数个数不可能为（　　）
A、3个B、4个C、5个D、6个
设f（x）与g（x）是定义在同一区间D上的两个函数，若?x0∈D，使得|f（x0）-g（x0）|≤1，则称f（x）和g（x）是D上的“接近函数”，D称为“接近区间”；若?x∈D，都有|f（x）-g（x）|＞1，则称f（x）和g（x）是D上的“远离函数”，D称为“远离区间”．给出以下命题：
①f（x）=x2+1与g（x）=x2+
3
2
是（-∞，+∞）上的“接近函数”；
②f（x）=x2-3x+4与g（x）=2x-3的一个“远离区间”可以是[2，3]；
③f（x）=
1-x2
和g（x）=-x+b（b＞
2
）是（-1，1）上的“接近函数”，则
2
＜b≤
2
+1；
④若f（x）=
lnx
x
+2ex与g（x）=x2+a+e2（e是自然对数的底数）是[1，+∞）上的“远离函数”，则a＞1+
2
e
．
其中的真命题有
 
．（写出所有真命题的序号）
根据工作需要，现从4名女教师，a名男教师中选3名教师组成一个援川团队，其中a=
∫
4
0
5
8
xdx，要求团队中男、女教师都有，则不同的组队方案种数为（　　）
A、140B、100
C、80D、70
若执行如图的程序框图，则输出的k值是（　　）
A、4B、5C、6D、7
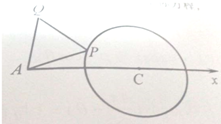若（x-1）5=a5（x+1）5+a4（x+1）4+a3（x+1）3+a2（x+1）2+a1（x+1）+a0，则a1+a2+a3+a4+a5=
 
．
已知半径为2的定圆C外一定点A，且AC=4，在圆上任取一点P，以AP为一边逆时针作等边△APQ，当P在圆上运动时，建立适当的极坐标系，求点Q轨迹的极坐标方程，并转化为直角坐标方程．
已知单调递增的等比数列{an}满足a2+a3+a4=28，a3+2是a2，a4的等差中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=anlog2an，sn=b1+b2+…+bn，求sn-n•2n+1+50＜0成立的正整数n的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网