题目内容
已知x>0,有下列不等式成立:x+
≥2
=2,x+
≥3
=3,…x+
≥n+1,据此归纳,则a= .
| 1 |
| x |
x•
|
| 4 |
| x2 |
|
| a |
| xn |
考点:归纳推理
专题:推理和证明
分析:根据题意,对给出的几个等式变形可得,x+
≥2
=2,x+
≥3
=3,…归纳可得变化规律,左式为x+
,右式为n+1,即可得答案.
| 1 |
| x |
x•
|
| 4 |
| x2 |
|
| nn |
| xn |
解答:
解:根据题意,对给出的等式变形可得,
x+
≥2
=2,
x+
≥3
=3,
…
归纳可得:一般的不等式为x+
≥n+1,(n是正整数);
故a=nn,
故答案为:nn(n是正整数).
x+
| 1 |
| x |
x•
|
x+
| 4 |
| x2 |
|
…
归纳可得:一般的不等式为x+
| nn |
| xn |
故a=nn,
故答案为:nn(n是正整数).
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
已知tanα,tanβ是关于x的方程x2+(logaM+logbM)x-logaM•logbM=0的两个根,其中a、b,M均为不等于1的正数,若sinαcosβ+cosαsinβ=2sinαsinβ,则a,b,M满足的关系是( )
A、
| ||
B、
| ||
| C、a+b=M | ||
| D、ab=M |
已知双曲线
-
=1(a>0,b>0)的右焦点F(2,0),设A,B为双曲线上关于原点对称的两点,以AB为直径的圆过点F,直线AB的斜率为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
3
| ||
| 7 |
A、
| ||
B、
| ||
| C、4 | ||
| D、2 |
如图是某几何体的三视图,则该几何体的体积为( )
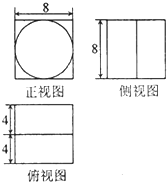

| A、256+128π |
| B、256+64π |
| C、64+64π |
| D、64+32π |
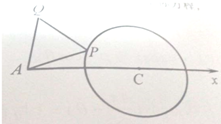 已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.
已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.