题目内容
8.某同学用“五点法”画函数f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$在某一个周期的图象时,列表并填入的部分数据如表:| x | $\frac{2}{3}$π | x1 | $\frac{8}{3}$π | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3}{2}$π | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(Ⅱ)若对任意的x1,x2∈[0,π],都有|f(x1)-f(x2)|<t恒成立,求实数t的取值范围.
分析 (I)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(Ⅱ)由题意可得f(x)∈[-$\sqrt{3}$,1],且|f(x1)-f(x2)|的最大值小于t,由此求得t的范围.
解答 解:(I)x1=$\frac{\frac{2π}{3}+\frac{8π}{3}}{2}$=$\frac{5π}{3}$,x1-$\frac{2π}{3}$=π,∴x2=$\frac{8π}{3}$+π=$\frac{11π}{3}$,x3=$\frac{11π}{3}$+π=$\frac{14π}{3}$.
由表格可得A=2,$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{8π}{3}$-$\frac{2π}{3}$,求得ω=$\frac{1}{2}$,再根据五点法作图可得$\frac{1}{2}$•$\frac{2π}{3}$+φ=0,求得φ=-$\frac{π}{3}$,
故函数f(x)=2sin($\frac{1}{2}$x-$\frac{π}{3}$).
(Ⅱ)若对任意的x1,x2∈[0,π],都有|f(x1)-f(x2)|<t恒成立,
故当x∈[0,π]时,$\frac{1}{2}$x∈[-$\frac{π}{3}$,$\frac{π}{6}$],∴f(x)∈[-$\sqrt{3}$,1],|f(x1)-f(x2)|的最大值小于t.
故 1-(-$\sqrt{3}$)<t,即 t>1+$\sqrt{3}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数的恒成立问题,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.已知直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
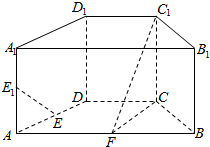 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.