题目内容
8.已知圆C:(x-3)2+(y-4)2=25,圆C上的点到直线l:3x+4y+m=0(m<0)的最短距离为1,若点N(a,b)在直线l位于第一象限的部分,则$\frac{1}{a}+\frac{1}{b}$的最小值为$\frac{{7+4\sqrt{3}}}{55}$.分析 求出圆的圆心与半径,利用圆C上的点到直线l:3x+4y+m=0(m<0)的最短距离为1,求出m,然后推出a,b的方程,利用基本不等式求解表达式的最值.
解答 解:圆C:(x-3)2+(y-4)2=25,圆心坐标(3,4),半径为5,
圆C上的点到直线l:3x+4y+m=0(m<0)的最短距离为1,
可得$\frac{|9+16+m|}{\sqrt{9+16}}$=6,解得m=-55.
点N(a,b)在直线l位于第一象限的部分,
可得3a+4b=55.
则$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{55}$($\frac{1}{a}+\frac{1}{b}$)(3a+4b)=$\frac{1}{55}$[7+$\frac{4b}{a}$+$\frac{3a}{b}$]≥$\frac{1}{55}$(7+$2\sqrt{\frac{4b}{a}•\frac{3a}{b}}$)=$\frac{{7+4\sqrt{3}}}{55}$.当且仅当3a2=4b2,a=$\frac{55(2\sqrt{3}-3)}{3}$取等号.
故答案为:$\frac{{7+4\sqrt{3}}}{55}$.
点评 本题考查与与圆的方程的应用,基本不等式求解表达式的最值,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
 如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )
如图是一个正三棱柱挖去一个圆柱得到的一个几何体的三视图,则该几何体的体积与挖去的圆柱的体积比为( )| A. | $\frac{{3\sqrt{3}}}{π}-1$ | B. | $\frac{{3\sqrt{3}}}{π}-\frac{1}{3}$ | C. | $\frac{{3\sqrt{3}}}{π}$ | D. | $\frac{{3\sqrt{3}}}{π}+1$ |
3.设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]⊆D(a<b),使f(x)在[a,b]上的值域也是[a,b],则称为“优美函数”,若函数$f(x)={log_2}({4^x}+t)$为“优美函数”,则t的取值范围是( )
| A. | $(\frac{1}{4},+∞)$ | B. | (0,1) | C. | $(0,\frac{1}{2})$ | D. | $(0,\frac{1}{4})$ |
13.6名学生和2位老师站成一排合影,其中2位老师不相邻的站法有( )种.
| A. | 30228 | B. | 30232 | C. | 30236 | D. | 30240 |
1.若圆x2+y2+dx+ey+f=0与两坐标轴都相切,则常数d,e,f之间的关系是( )
| A. | d≠0且e2=4f | B. | d≠0且e2≠4f | C. | d=e且e2≠4f | D. | d2=e2=4f>0 |
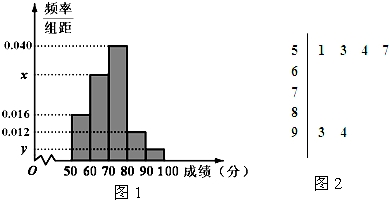
 某厂商调查甲、乙两种不同型号电视在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”
某厂商调查甲、乙两种不同型号电视在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”