题目内容
由下列条件求双曲线的标准方程:
(1)两焦点坐标为(-5,0),(5,0),双曲线上一点P与两焦点距离的差的绝对值为8;
(2)两焦点坐标为(0,-6),(0,6),且双曲线过点(-5,6).
(1)两焦点坐标为(-5,0),(5,0),双曲线上一点P与两焦点距离的差的绝对值为8;
(2)两焦点坐标为(0,-6),(0,6),且双曲线过点(-5,6).
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意设双曲线的标准方程为
-
=1,a>0,b>0,由已知得
,由此能求出双曲线的标准方程.
(2)由题意设双曲线的标准方程为
-
=1,a>0,b>0,由已知得
,由此能求出双曲线的标准方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)由题意设双曲线的标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
|
解答:
解:(1)由题意设双曲线的标准方程为
-
=1,a>0,b>0,
由已知得
,解得a=4,b=3,
∴双曲线的标准方程为
-
=1.
(2)由题意设双曲线的标准方程为
-
=1,a>0,b>0,
由已知得
,
解得a=4,b=2
,
∴双曲线的标准方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
由已知得
|
∴双曲线的标准方程为
| x2 |
| 16 |
| y2 |
| 9 |
(2)由题意设双曲线的标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
由已知得
|
解得a=4,b=2
| 5 |
∴双曲线的标准方程为
| y2 |
| 16 |
| x2 |
| 20 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,注意双曲线的性质的合理运用.

练习册系列答案
相关题目
已知数列{an}满足a1=1且
=
,则a2012=( )
| an+1 |
| an |
| n+1 |
| n |
| A、2 010 |
| B、2 011 |
| C、2 012 |
| D、2 013 |
已知f(x)是周期为4的奇函数,f(3)=2,则f(9)=( )
| A、6 | B、-6 | C、2 | D、-2 |
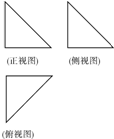 已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )A、6+2
| ||
B、6+4
| ||
C、12+4
| ||
D、8+4
|
已知双曲线
-
=1的焦点为(4,0),则此双曲线的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| 4 |
A、
| ||
B、x±
| ||
C、
| ||
D、x±
|
设a=
,b=tan10°+tan50°+
tan10°•tan50°,则下列各式正确的为( )
| 1+tan10° |
| 1-tan10° |
| 3 |
A、a<b<
| ||
B、a<
| ||
C、b<
| ||
D、b<a<
|