题目内容
已知椭圆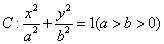 的两个焦点分别为
的两个焦点分别为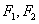 ,且
,且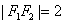 ,点
,点 在椭圆上,且
在椭圆上,且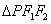 的周长为6。
的周长为6。
(1)求椭圆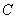 的方程;
的方程;
(2)若点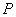 的坐标为
的坐标为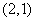 ,不过原点
,不过原点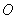 的直线
的直线 与椭圆
与椭圆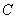 相交于
相交于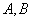 两点,设线段
两点,设线段 的中点为
的中点为 ,点
,点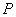 到直线
到直线 的距离为
的距离为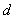 ,且
,且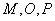 三点共线。求
三点共线。求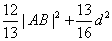 的最大值
的最大值
解:(1)由已知得 ,且
,且 ,解得
,解得 ,又
,又
所以椭圆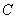 的方程为
的方程为 ……………………3分
……………………3分
(2)当直线 与
与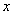 轴垂直时,由椭圆的对称性可知:
轴垂直时,由椭圆的对称性可知:
点 在
在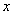 轴上,且原点
轴上,且原点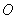 不重合,显然
不重合,显然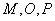 三点不共线,不符合题设条件。
三点不共线,不符合题设条件。
所以可设直线 的方程为
的方程为 ,
,
由 消去
消去 并整理得:
并整理得: ……………① 6分
……………① 6分
则 ,即
,即 ,设
,设 ,
,
且 ,则点
,则点 ,
,
因为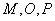 三点共线,则
三点共线,则 ,即
,即 ,而
,而 ,所以
,所以 ……………9分
……………9分
此时方程①为 ,且
,且
所以
又
所以
故当 时,
时,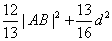 的最大值为
的最大值为 ……………………
……………………

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
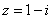 (
(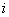 是虚数单位),则复数
是虚数单位),则复数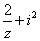 的虚部是( )
的虚部是( )  B.
B.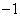 C.
C.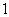
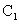 的中心在原点,焦点在x轴上,若
的中心在原点,焦点在x轴上,若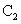 :
: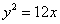 的焦点重合,且抛物线
的焦点重合,且抛物线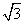 ,则双曲线
,则双曲线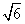 C.
C.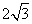
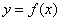 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有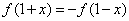 .当
.当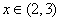 时,
时,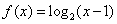
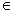 Z)成中心对称;
Z)成中心对称; 是以2为周期的周期函数;
是以2为周期的周期函数; 时,
时,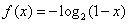 ;
;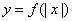 在(k,k+1)( k
在(k,k+1)( k D. 2014
D. 2014
 相交于A,B两点,则|AB|的最小值为( )
相交于A,B两点,则|AB|的最小值为( ) B.4 C.
B.4 C.  D.5
D.5 中,
中, ,
, ,则
,则 .
.