题目内容
已知函数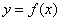 为奇函数,且对定义域内的任意x都有
为奇函数,且对定义域内的任意x都有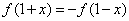 .当
.当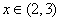 时,
时,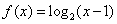
给出以下4个结论:
①函数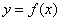 的图象关于点(k,0)(k
的图象关于点(k,0)(k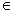 Z)成中心对称;
Z)成中心对称;
②函数 是以2为周期的周期函数;
是以2为周期的周期函数;
③当 时,
时,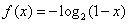 ;
;
④函数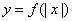 在(k,k+1)( k
在(k,k+1)( k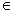 Z)上单调递增.
Z)上单调递增.
其一中所有正确结论的序号为
①②③
【解析】试题分析:由题设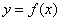 为奇函数,其图象关于原点中心对称,
为奇函数,其图象关于原点中心对称,
又对定义域内的任意x都有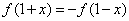 ,所以其图象还关于点
,所以其图象还关于点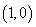 ,据此可判断函数
,据此可判断函数 为周期函数,最小正周期
为周期函数,最小正周期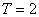 ,又当
,又当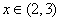 时,
时,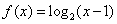 ,因此可画出函数
,因此可画出函数 的图象大致如下图一所示,函数
的图象大致如下图一所示,函数 的图象如下图二所示,函数
的图象如下图二所示,函数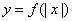 的图象如下图三所示,
的图象如下图三所示,
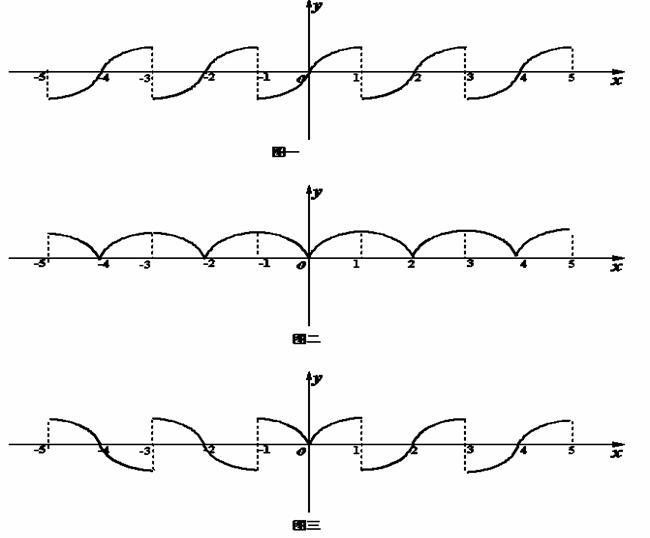
由图象可知①②正确,④不正确;
另外,当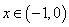 时,
时,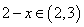
所以,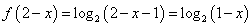
又因为 是以2这周期的奇函数
是以2这周期的奇函数
所以,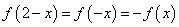
所以,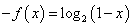
所以,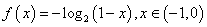 ,所以③也正确
,所以③也正确
故答案应填:①②③
考点: 函数的图象与性质的综合应用

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
,  、
、 分别是
分别是 、
、 的中点,主(正)视图方向垂直平面
的中点,主(正)视图方向垂直平面 .
. ⑴求证:
⑴求证: ∥平面
∥平面 ;
;
 平面
平面 ,若z的最小值为3,则m的值为( )
,若z的最小值为3,则m的值为( )
 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数的取值范围为( )
恒成立,则实数的取值范围为( )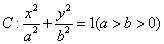 的两个焦点分别为
的两个焦点分别为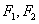 ,且
,且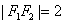 ,点
,点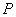 在椭圆上,且
在椭圆上,且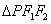 的周长为6。
的周长为6。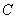 的方程;
的方程;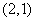 ,不过原点
,不过原点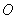 的直线
的直线 与椭圆
与椭圆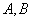 两点,设线段
两点,设线段 的中点为
的中点为 ,点
,点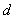 ,且
,且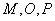 三点共线。求
三点共线。求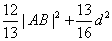 的最大值
的最大值 的图象大致为 ( )
的图象大致为 ( )
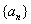 的前
的前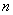 项和为
项和为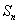 ,点
,点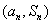 在直线
在直线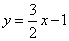 上.
上.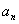 与
与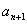 之间插入
之间插入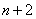 个数组成公差为
个数组成公差为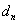 的等差数列,
的等差数列,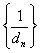 的前
的前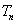 ,并求使
,并求使 成立的正整数
成立的正整数