题目内容
已知在△ABC中,AB=3,∠A=60°,∠A的平分线AD交边BC于点D,且
=λ
+
(λ∈R),则AD的长为( )
| AD |
| AC |
| 1 |
| 6 |
| AB |
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
考点:平面向量的基本定理及其意义,向量加减混合运算及其几何意义
专题:平面向量及应用
分析:如图所示,过点D分别作DE∥AC交AB于点E,DF∥AB交AC于点F,由于B,D,C三点在同一条直线上,可得λ+
=1.又
=
,可得AC=
.再利用数量积的性质即可得出.
| 1 |
| 6 |
| AB |
| AC |
| BD |
| DC |
| 3 |
| 5 |
解答:
解:如图所示,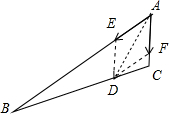
过点D分别作DE∥AC交AB于点E,DF∥AB交AC于点F,
∵B,D,C三点在同一条直线上,则λ+
=1,
∴λ=
.
又
=
=
=5,∴AC=
.
∴
2=(
+
)2=
2+
2+2×
×
×|
| |
|cos60°
=
×
+
×9+
×
×3×
=
.
∴|
|=
.
故选:A.

过点D分别作DE∥AC交AB于点E,DF∥AB交AC于点F,
∵B,D,C三点在同一条直线上,则λ+
| 1 |
| 6 |
∴λ=
| 5 |
| 6 |
又
| AB |
| AC |
| BD |
| DC |
| ||
|
| 3 |
| 5 |
∴
| AD |
| 5 |
| 6 |
| AC |
| 1 |
| 6 |
| AB |
| 25 |
| 36 |
| AC |
| 1 |
| 36 |
| AB |
| 5 |
| 6 |
| 1 |
| 6 |
| AC |
| AB |
=
| 25 |
| 36 |
| 9 |
| 25 |
| 1 |
| 36 |
| 5 |
| 18 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 4 |
∴|
| AD |
| ||
| 2 |
故选:A.
点评:本题考查了向量共线定理、平行四边形法则、角平分线性质定理、数量积的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
在平面直角坐标系中,不等式
(a为常数)表示的平面区域的面积为8,则
的最小值为( )
|
| x+y+2 |
| x+3 |
A、8
| ||
B、5-4
| ||
C、6-4
| ||
D、
|
在△ABC中,
•
=
•
,则△ABC是( )
| CB |
| CA |
| BC |
| BA |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、等腰三角形 |
| D、直角三角形 |
阅读如图的程序框图,运行相应的程序,若输出S=
,则判断框内应填入( )

| 2013 |
| 2014 |

| A、i≥2014 |
| B、i≥2015 |
| C、i>2014 |
| D、i>2015 |
若用C、R和I分别表示复数集、实数集和纯虚数集,其中C为全集,那么有( )
| A、C=R∪I |
| B、R∪∁CI=R |
| C、∁CR=C∩I |
| D、∁CR∩I=I |
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积为( )


| A、30 | B、24 | C、10 | D、6 |
已知函数f(x)=
,若存在实数t使得f(x)在R上为单调函数,则a的取值范围是( )
|
| A、a≥0 | B、a<0 |
| C、a≤t | D、a<-t |
执行如图所示的程序框图,输出的结果是15,则a的初始值m(m>0)有多少种可能( )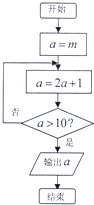

| A、1 | B、2 | C、3 | D、4 |