题目内容
已知函数f(x)=ax2+bx+c(a≠0)满足f(0)=-4,f(x+1)为偶函数,且x=-2是函数f(x)-4的一个零点.又g(x)=mx+4(m>0).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若关于x的方程f(x)=g(x)在x∈(1,5)上有解,求实数m的取值范围;
(Ⅲ)令h(x)=f(x)-|g(x)|,求h(x)的单调区间.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若关于x的方程f(x)=g(x)在x∈(1,5)上有解,求实数m的取值范围;
(Ⅲ)令h(x)=f(x)-|g(x)|,求h(x)的单调区间.
考点:函数解析式的求解及常用方法,函数的零点
专题:分类讨论,函数的性质及应用
分析:(Ⅰ)由f(0)求出c的值,由f(x+1)为偶函数,且x=-2是函数f(x)-4的一个零点,求出a、b的值,即得f(x);
(Ⅱ)方程x2-2x-4=mx+4在x∈(1,5)上有解,转化为求m=x-2-
在(1,5)上的取值范围;
(Ⅲ)求出h(x)的表达式,讨论m的取值,对应函数h(x)的单调性是什么,写出对应的单调区间.
(Ⅱ)方程x2-2x-4=mx+4在x∈(1,5)上有解,转化为求m=x-2-
| 8 |
| x |
(Ⅲ)求出h(x)的表达式,讨论m的取值,对应函数h(x)的单调性是什么,写出对应的单调区间.
解答:
解:(Ⅰ)∵f(0)=-4,∴c=-4;(1分)
∵f(x+1)=a(x+1)2+b(x+1)+c,
即f(x+1)=ax2+(2a+b)x+a+b+c;
又∵f(x+1)为偶函数,∴2a+b=0;①(2分)
∵x=-2是函数f(x)-4的一个零点,
∴f(-2)-4=0,∴4a-2b-8=0;②
由①②解得a=1,b=-2;
∴f(x)=x2-2x-4;(4分)
(Ⅱ)f(x)=g(x)在x∈(1,5)上有解,
即x2-2x-4=mx+4在x∈(1,5)上有解;
∴m=x-2-
;
∵m=x-2-
在(1,5)上单调递增,
∴实数m的取值范围为(-9,
);(8分)
(Ⅲ)h(x)=x2-2x-4-|mx+4|,
即h(x)=
;(9分)
①当x≥-
时,h(x)=x2-(m+2)x-8的对称轴为x=
,
∵m>0,∴
>-
总成立;
∴h(x)在(-
,
)上单调递减,在(
,+∞)上单调递增;(11分)
②当x<-
时,h(x)=x2+(m-2)x的对称轴为x=
,
若
≥-
,即0<m≤4,h(x)在(-∞,-
)上单调递减;(13分)
若
<-
,即m>4,h(x)在(-∞,
)上单调递减,在(
,-
)上单调递增;(15分)
综上,当0<m≤4时,h(x)的单调递减区间为(-∞,
),单调递增区间为(
,+∞);
当m>4时,h(x)的单调递减区间为(-∞,
)和(-
,
);单调递增区间为(
,-
)和(
,+∞).(16分)
∵f(x+1)=a(x+1)2+b(x+1)+c,
即f(x+1)=ax2+(2a+b)x+a+b+c;
又∵f(x+1)为偶函数,∴2a+b=0;①(2分)
∵x=-2是函数f(x)-4的一个零点,
∴f(-2)-4=0,∴4a-2b-8=0;②
由①②解得a=1,b=-2;
∴f(x)=x2-2x-4;(4分)
(Ⅱ)f(x)=g(x)在x∈(1,5)上有解,
即x2-2x-4=mx+4在x∈(1,5)上有解;
∴m=x-2-
| 8 |
| x |
∵m=x-2-
| 8 |
| x |
∴实数m的取值范围为(-9,
| 7 |
| 5 |
(Ⅲ)h(x)=x2-2x-4-|mx+4|,
即h(x)=
|
①当x≥-
| 4 |
| m |
| m+2 |
| 2 |
∵m>0,∴
| m+2 |
| 2 |
| 4 |
| m |
∴h(x)在(-
| 4 |
| m |
| m+2 |
| 2 |
| m+2 |
| 2 |
②当x<-
| 4 |
| m |
| 2-m |
| 2 |
若
| 2-m |
| 2 |
| 4 |
| m |
| 4 |
| m |
若
| 2-m |
| 2 |
| 4 |
| m |
| 2-m |
| 2 |
| 2-m |
| 2 |
| 4 |
| m |
综上,当0<m≤4时,h(x)的单调递减区间为(-∞,
| m+2 |
| 2 |
| m+2 |
| 2 |
当m>4时,h(x)的单调递减区间为(-∞,
| 2-m |
| 2 |
| 4 |
| m |
| m+2 |
| 2 |
| 2-m |
| 2 |
| 4 |
| m |
| m+2 |
| 2 |
点评:本题考查了求函数的解析式以及函数的单调性与奇偶性问题,解题时应用分类讨论思想,是较难的题目.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
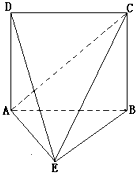 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE= 已知函数f(x)=2cosxsin(x+
已知函数f(x)=2cosxsin(x+