题目内容
11．已知等差数列{an}满足a3•a7=-12，a4+a6=-4，求等差数列{an}的通项公式．分析 由已知得a3，a7是一元二次方程x2+4x-12=0的两个根，解方程x2+4x-12=0，得x1=-6，x2=2，从而得到a3=-6，a7=2或a3=2，a7=-6，由此能求出数列{an}的通项公式．
解答 解：∵等差数列{an}满足a3•a7=-12，a4+a6=a3+a7=-4，
∴a3，a7是一元二次方程x2+4x-12=0，
解方程x2+4x-12=0，得x1=-6，x2=2，
当a3=-6，a7=2时，
$\left\{\begin{array}{l}{{a}_{1}+2d=-6}\\{{a}_{1}+6d=2}\end{array}\right.$，解得a1=-10，d=2，
an=-10+（n-1）×2=2n-12；
当a3=2，a7=-6时，
$\left\{\begin{array}{l}{{a}_{1}+2d=2}\\{{a}_{1}+6d=-6}\end{array}\right.$，解得a1=6，d=-2，
an=6+（n-1）×（-2）=-2n+8．
点评 本题考查等差数列的通项公式，解题时要认真审题，注意等差数列的性质的合理运用，是基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
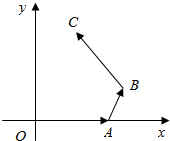如图，在平面直角坐标系中，$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$，∠OAB=$\frac{2π}{3}$，$\overrightarrow{BC}=（-1，\sqrt{3}）$，求点B，C的坐标．
2．若数列{an}是公比为q的等比数列，下列数列中不是等比数列的是（ ）
| A． | {an•an+1} | B． | {nan} | C． | {${a}_{n}^{2}$} | D． | $\frac{{a}_{n}}{{a}_{n+1}}$ |