题目内容

6．数列{an}中，an=$\frac{1}{n+1}$-$\frac{1}{n}$，则a1+a2+a3+…a100=$-\frac{100}{101}$．

分析 直接利用数列的通项公式表示数列的和，求解即可．

解答 解：数列{an}中，an=$\frac{1}{n+1}$-$\frac{1}{n}$，
则a1+a2+a3+…a100=$\frac{1}{2}-1$$+\frac{1}{3}-\frac{1}{2}$+$\frac{1}{4}$$-\frac{1}{3}$+…+$\frac{1}{101}$-$\frac{1}{100}$=-1+$\frac{1}{101}$=-$\frac{100}{101}$．
故答案为：$-\frac{100}{101}$．

点评 本题考查数列求和，裂项法的应用，考查计算能力．

练习册系列答案
相关题目
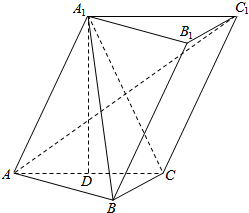16．已知三棱柱ABC-A1B1C1，A1在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，又知BA1⊥AC1
（1）求证：AC1⊥平面A1BC；
（2）求以△ABA1为底面的三棱锥C-ABA1的高．
17．已知A={x|-1＜x＜2}，B={x|x≤1}，则A∩（∁RB）=（　　）
A．{x|1＜x＜2}B．{x|-1＜x＜1}C．{x|-1＜x＜2}D．{x|1≤x＜2}
14．已知函数f（x）=msinx+ncosx（m，n为常数，m，n≠0）的一个极大值点为$\frac{π}{4}$，若函数y=f（$\frac{π}{3}$-ωx）的图象关于点（$\frac{7π}{12}$，0）中心对称，则ω的值不可能为（　　）
A．1B．2C．13D．-$\frac{5}{7}$
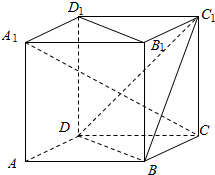1．如图，ABCD-A1B1C1D1是棱长为1正方体．
（1）求证：B1D1∥面C1BD；
（2）求证：A1C⊥平面C1BD．
11．已知等差数列{an}满足a3•a7=-12，a4+a6=-4，求等差数列{an}的通项公式．
18．已知函数f（x）=2sin（2x-$\frac{π}{3}$）+1．
（Ⅰ）求函数f（x）图象的对称轴的方程和对称中心的坐标；
（Ⅱ）求函数f（x）在[-$\frac{π}{2}$，$\frac{π}{2}$]上的单调递增区间；
（Ⅲ）求函数f（x）在[0，$\frac{π}{2}$]上的值域．
15．设命题p：?x∈[1，2]，x-lnx-a＜1为真命题，则实数a的取值范围为a＞1-ln2．
19．已知函数$f（x）=\frac{sin2x+cos2x+1}{2cosx}$
（Ⅰ）求函数f（x）的定义域
（Ⅱ）若$f（{α+\frac{π}{4}}）=\frac{{3\sqrt{2}}}{5}$，求cosα的值
（Ⅲ）在（Ⅱ）条件下，若α是第四象限角，求$cos（{π-2α}）+cos（{2α-\frac{π}{2}}）$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网