题目内容
1.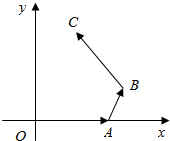 如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.
如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.
分析 由题意,求出AB的倾斜角$\frac{π}{3}$,即可求出点B的坐标,再设点C的坐标(x,y),由向量$\overrightarrow{BC}$列方程组,求出x,y的值.
解答 解:平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,
∴AB的倾斜角为$\frac{π}{3}$,|$\overrightarrow{AB}$|=1,
∴点B的坐标为($\frac{5}{2}$,$\frac{\sqrt{3}}{2}$);
设点C(x,y),
∴$\overrightarrow{BC}$=(x-$\frac{5}{2}$,y-$\frac{\sqrt{3}}{2}$)=(-1,$\sqrt{3}$),
即$\left\{\begin{array}{l}{x-\frac{5}{2}=-1}\\{y-\frac{\sqrt{3}}{2}=\sqrt{3}}\end{array}\right.$,
解得x=$\frac{3}{2}$,y=$\frac{3\sqrt{3}}{2}$;
∴点C的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
点评 本题考查直线的倾斜角的求法,向量的坐标与向量的模,体现了数形结合的数学思想.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.用区间表示|x|<5的解集是( )
| A. | (-∞,5) | B. | (5,+∞) | C. | (0,5) | D. | (-5,5) |
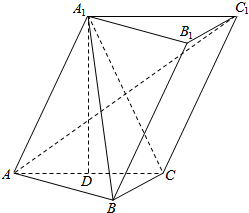 已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1