题目内容
4.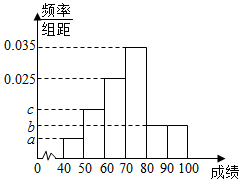 已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.(1)求n的值;
(2)若成绩在[40,50)内的人数是成绩在[50,60)内的人数的$\frac{1}{3}$,规定60分以下为不及格,从不及格的人中任意选取3人,求成绩在50分以下的人数X的分布列和数学期望.
分析 (1)由频率分布直方图和等差数列的性质求出b=0.01,再由成绩在[90,100]内的有6人,能求出n.
(2)求出a=0.005,c=0.015,从而得到不及格的人数为18人,其中成绩在50分以下的人数为3人,从不及格的人中任意选取3人,成绩在50分以下的人数X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)由频率分布直方图,得:
$\left\{\begin{array}{l}{2b=a+c}\\{(a+2b+c+0.025+0.035)×10=1}\end{array}\right.$,
解得b=0.01,
∵成绩在[90,100]内的有6人,∴$\frac{6}{n}=0.1$,解得n=60.
(2)∵成绩在[40,50)内的人数是成绩在[50,60)内的人数的$\frac{1}{3}$,
∴a=0.005,c=0.015,
∴规定60分以下为不及格,则不及格的人数为(0.005+0.01+0.015)×10×60=18,
其中成绩在50分以下的人数为0.05×10×60=3人,
∴从不及格的人中任意选取3人,成绩在50分以下的人数X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{15}^{3}}{{C}_{18}^{3}}$=$\frac{455}{816}$,
P(X=1)=$\frac{{C}_{3}^{1}{C}_{15}^{2}}{{C}_{18}^{3}}$=$\frac{315}{816}$,
P(X=2)=$\frac{{C}_{3}^{2}{C}_{15}^{1}}{{C}_{18}^{3}}$=$\frac{45}{816}$,
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{18}^{3}}$=$\frac{1}{816}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{455}{816}$ | $\frac{315}{816}$ | $\frac{45}{816}$ | $\frac{1}{816}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案| A. | 6 | B. | 24 | C. | 48 | D. | 120 |
| A. | [$\frac{14}{3}$,$\frac{37}{3}$] | B. | [$\frac{1}{3}$,$\frac{50}{3}$] | C. | [$\frac{11}{3}$,6] | D. | [$\frac{41}{6}$,$\frac{22}{3}$] |
| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [0,$\frac{1}{3}$] | D. | [0,$\frac{4}{3}$] |

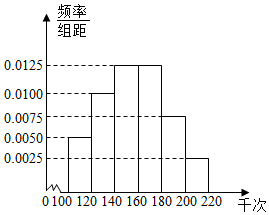 2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示
2015年12月16日到18日第二届世界互联网大会在乌镇举行,17日奇虎360董事长周鸿祎在回答海外网记者的提问时,分享了过去100天中国每天遭受DDOS攻击的次数数据,并根据数据作出频率分布直方图,如图所示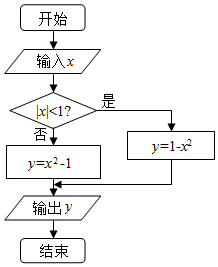 如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.
如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.