题目内容
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )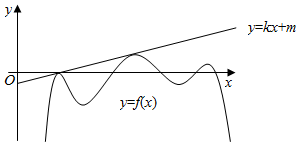
| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
分析 对函数F(x)=f(x)-kx,求导数,根据条件判断f′(x)与k的关系进行判断即可.
解答 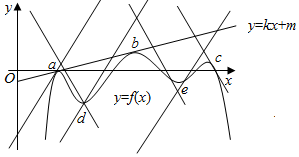 解:∵直线y=kx+m与曲线y=f(x)相切于两点,
解:∵直线y=kx+m与曲线y=f(x)相切于两点,
∴kx+m=f(x)有两个根,且f(x)≤kx+m,
由图象知m<0,
则f(x)<kx,
即则F(x)=f(x)-kx<0,则函数F(x)=f(x)-kx,没有零点,
函数f(x)有3个极大值点,2个极小值点,
则F′(x)=f′(x)-k,
设f(x)的三个极大值点分别为a,b,c,
则在a,b,c的左侧,f′(x)>k,a,b,c的右侧f′(x)<k,此时函数F(x)=f(x)-kx有3个极大值,
在d,e的左侧,f′(x)<k,d,e的右侧f′(x)>k,此时函数F(x)=f(x)-kx有2个极小值,
故函数F(x)=f(x)-kx有5个极值点,3个极大值,2个极小值,
故选:D
点评 本题主要考查函数零点的判断以及极值的判断,利用图象求函数的导数,利用函数极值和导数之间的关系是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.A,B,C,D,E五人并排站成-行,如果A,B必须相邻且B在A的右边.耶么不同的排法种数是( )
| A. | 6 | B. | 24 | C. | 48 | D. | 120 |
20.已知ω>0,函数f(x)=sin(ωx+$\frac{5π}{6}$)的一条对称轴为直线x=$\frac{π}{3}$,一个对称中心是($\frac{π}{12}$,0),则ω有( )
| A. | 最小值2 | B. | 最大值2 | C. | 最小值1 | D. | 最大值1 |
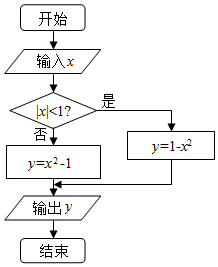 如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.
如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.