题目内容
16.已知函数$f(x)=\frac{1+lnx}{x}$,证明:f(x)≤1.分析 令g(x)=lnx-x+1,g'(x)=$\frac{1}{x}$-1,确定函数的单调性,证明g(x)=lnx-x+1≤g(1)=0,即可证明结论.
解答 证明:f(x)≤1,只需要证明 lnx+1≤x.
令g(x)=lnx-x+1,g'(x)=$\frac{1}{x}$-1
x≥1时,g'(x)≤0,所以g(x)是减函数;0<x<1时,g'(x)>0,g(x)是增函数,
所以g(x)=lnx-x+1≤g(1)=0,
∴lnx+1≤x,∴$f(x)=\frac{1+lnx}{x}$.
点评 本题考查不等式的证明,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.已知实数m是2,8的等比中项,则双曲线x2-$\frac{{y}^{2}}{m}$=1的一条渐近线方程为( )
| A. | y=4x | B. | y=$\frac{1}{4}$x | C. | y=2x | D. | y=$\frac{1}{2}$x |
7.已知向量$\overrightarrow a$,$\overrightarrow b$的夹角为120°,且$|{\overrightarrow a}|=2,|{\overrightarrow b}|=5$,则$({2\overrightarrow a-\overrightarrow b})•\overrightarrow a$等于( )
| A. | 12 | B. | $8+\sqrt{13}$ | C. | 4 | D. | 13 |
11.设x,y∈R,则“x≥2且y≥2”是“x+y≥4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
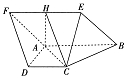 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.