题目内容
1.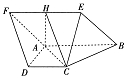 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.(1)求证:FD∥平面AHC;
(2)求多面体ABCDEF的体积.
分析 (1)由∠BAD=∠CDA=90°,可得AB∥CD,再由四边形ABEF为菱形,可得AB∥EF,得到EF∥CD.结合H是EF的中点,AB=2CD,得CD=FH,可得四边形CDFH为平行四边形,从而得到DF∥CH.再由线面平行的判定可得FD∥平面AHC;
(2)由平面ABEF⊥平面ABCD,DA⊥AB,可得DA⊥平面ABEF,结合已知可得四棱锥C-ABEF的高DA=2,三棱锥F-ADC的高AH=$\sqrt{3}$.然后由VABCDEF=VC-ABEF+VF-ADC求得多面体ABCDEF的体积.
解答 (1)证明:∵∠BAD=∠CDA=90°,∴AB∥CD,
∵四边形ABEF为菱形,∴AB∥EF,则EF∥CD.
∵H是EF的中点,AB=2CD,∴CD=FH,
∴四边形CDFH为平行四边形,则DF∥CH.
∵DF?平面AHC,HC?平面AHC,
∴FD∥平面AHC;
(2)解:∵平面ABEF⊥平面ABCD,DA⊥AB,
∴DA⊥平面ABEF,
∵DC∥AB,∴四棱锥C-ABEF的高DA=2,
∵∠ABE=60°,四边形ABEF为边长是4的菱形,
∴可求三棱锥F-ADC的高AH=2$\sqrt{3}$.
∴VABCDEF=VC-ABEF+VF-ADC=$\frac{1}{3}×4×2\sqrt{3}×2+\frac{1}{3}×\frac{1}{2}×2×2×2\sqrt{3}$=$\frac{20\sqrt{3}}{3}$.
点评 本题考查线面平行的判定,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
6.某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制,各等制划分标准如表所示:
同时认定A,B,C为合格,D为不合格.已知甲,乙两所学校学生的原始成绩均分布在[50,100]内,为了比较两校学生的成绩,分别抽取100名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C,D的所有数据茎叶图如图2所示.
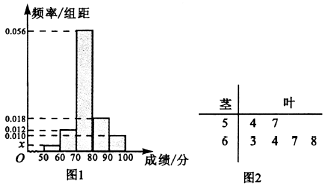
(1)求图中x的值,并根据样本数据比较甲乙两校的合格率;
(2)在乙校的样本中,从成绩等级为C的学生中随机抽取2名学生,从成绩等级为D的学生中随机抽取1名学生进行调研,求抽出的3名学生中恰有1名学生成绩在65分以上的概率.
| 分数 | [85,100] | [70,85) | [60,70) | [0,60) |
| 等级 | A等 | B等 | C等 | D等 |

(1)求图中x的值,并根据样本数据比较甲乙两校的合格率;
(2)在乙校的样本中,从成绩等级为C的学生中随机抽取2名学生,从成绩等级为D的学生中随机抽取1名学生进行调研,求抽出的3名学生中恰有1名学生成绩在65分以上的概率.
13.如果在犯错误的概率不超过0.05的前提下说事件A和B有关系,那么具体计算出的数据是( )
| A. | χ2≥3.841 | B. | χ2≤3.841 | C. | χ2≥6.635 | D. | χ2≤6.635 |
10.在锐角△ABC中,a=1,B=2A,则b的取值范围是( )
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{2},\sqrt{3})$ | C. | $(\sqrt{2},2)$ | D. | $(\sqrt{3},2)$ |
11.已知集合A={-1,0,1,2},集合B={y|y=2x-3,x∈A},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,1} | C. | {-1,1,2} | D. | {0,1,2} |