题目内容
11.设x,y∈R,则“x≥2且y≥2”是“x+y≥4”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据充分必要条件的定义判断即可.
解答 解:由x≥2且y≥2”推出“x+y≥4”,是充分条件,
由x+y≥4推不出x≥2且y≥2,比如x=1,y=5,故不是必要条件,
故选:A.
点评 本题考查了充分必要条件,考查不等式的性质,是一道基础题.

练习册系列答案
相关题目
1.直线ax+y-5=0截圆C:x2+y2-4x-2y+1=0的弦长为4,则a=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
2.不等式x+y-1>0表示的区域在直线x+y-1=0的( )
| A. | 左上方 | B. | 左下方 | C. | 右上方 | D. | 右下方 |
19.如图是某一几何体的三视图,则这个几何体的侧面积和体积分别是( )


| A. | 8$\sqrt{2}$+2$\sqrt{5}$+6,8 | B. | 2$\sqrt{2}$+8$\sqrt{5}$+6,8 | C. | 4$\sqrt{2}$+8$\sqrt{5}$+12,16 | D. | 8$\sqrt{2}$+4$\sqrt{5}$+12,16 |
3.现有1名男同学和2名女同学参加演讲比赛,共有2道演讲备选题目,若每位选手从中有放回地随机选出一道题进行演讲,以下说法不正确的是( )
| A. | 三人都抽到同一题的概率为$\frac{1}{4}$ | |
| B. | 只有两名女同学抽到同一题的概率为$\frac{1}{4}$ | |
| C. | 其中恰有一男一女抽到同一道题的概率为$\frac{1}{2}$ | |
| D. | 至少有两名同学抽到同一题的概率为$\frac{3}{4}$ |
20.已知函数y=2sin(ωx+φ)为偶函数(0<φ<π),其图象与直线y=2相邻的两个交点的横坐标分别为x1,x2且|x1-x2|=π则( )
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ | D. | ω=2,φ=$\frac{π}{4}$ |
1.已知f(x)是定义在R上的奇函数,且周期为2,当x∈(0,1]时,f(x)=1-x,则函数f(x)在[0,2017]上的零点个数是( )
| A. | 1008 | B. | 1009 | C. | 2017 | D. | 2018 |
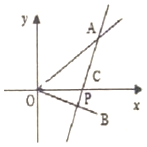 如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.
如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.