题目内容
5.当x∈[-1,2]时,x3-x2-x<m恒成立,则实数m的取值范围是(2,+∞).分析 当x∈[-1,2]时,x3-x2-x<m恒成立,即实数m大于左边函数的最大值,利用导数法可求.
解答 解:由题意,令f(x)=x3-x2-x,
∴f′(x)=3x2-2x-1,
令 f′(x)=3x2-2x-1=0,得x=1或x=-$\frac{1}{3}$,
当x∈(-1,-$\frac{1}{3}$)∪(1,2)时 f′(x)>0,当x∈($-\frac{1}{3},1$)时,f′(x)<0.
∴f(x)的增区间为(-1,-$\frac{1}{3}$),(1,2);减区间为($-\frac{1}{3},1$).
∵f(-$\frac{1}{3}$)=$\frac{5}{27}$,f(2)=2.
∴f(x)=x3-x2-x在x∈[-1,2]上的最大值为2.
∴实数m的取值范围是m>2.
故答案为:(2,+∞).
点评 本题考查函数恒成立问题,考查利用导数研究函数在闭区间上的最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果在犯错误的概率不超过0.05的前提下说事件A和B有关系,那么具体计算出的数据是( )
| A. | χ2≥3.841 | B. | χ2≤3.841 | C. | χ2≥6.635 | D. | χ2≤6.635 |
20.已知函数y=2sin(ωx+φ)为偶函数(0<φ<π),其图象与直线y=2相邻的两个交点的横坐标分别为x1,x2且|x1-x2|=π则( )
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ | D. | ω=2,φ=$\frac{π}{4}$ |
10.在锐角△ABC中,a=1,B=2A,则b的取值范围是( )
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{2},\sqrt{3})$ | C. | $(\sqrt{2},2)$ | D. | $(\sqrt{3},2)$ |
17.某几何体的三视图如图所示,则它的外接球表面积为( )


| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
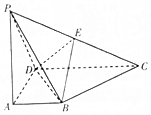 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.