题目内容
已知函数f(x)=x3-bx2+cx(b,c∈R),其图象记为曲线C.
(Ⅰ)若f(x)在x=1处取得极值-1,求b,c的值;
(Ⅱ)若f(x)有三个不同的零点,分别为x1,x2,x3,且x3>x2>x1=0,过点O(x1,f(x1))作曲线C的切线,切点为A(x0,f(x0))(点A异于点O).
(i)证明:x0=
(ii)若三个零点均属于区间[0,2),求
的取值范围.
(Ⅰ)若f(x)在x=1处取得极值-1,求b,c的值;
(Ⅱ)若f(x)有三个不同的零点,分别为x1,x2,x3,且x3>x2>x1=0,过点O(x1,f(x1))作曲线C的切线,切点为A(x0,f(x0))(点A异于点O).
(i)证明:x0=
| x2+x3 |
| 2 |
(ii)若三个零点均属于区间[0,2),求
| f(x0) |
| x0 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,根据函数极值和导数只记得关系建立条件关系即可求b,c的值;
(Ⅱ)求函数的导数,根据导数的几何意义转化为一元二次方程,以及线性规划的知识进行求解即可.
(Ⅱ)求函数的导数,根据导数的几何意义转化为一元二次方程,以及线性规划的知识进行求解即可.
解答:
解:(Ⅰ)函数的导数f′(x)=3x2-2bx+c,
若f(x)在x=1处取得极值-1,
则
,解得b=1,c=-1;
经检验知此时函数f(x)满足条件.
(Ⅱ)(i)证明:切线斜率k=f′(x0)=3x02-2bx0+c,
则切线方程为y-f(x0)=(3x02-2bx0+c)(x-x0),
化简得y=(3x02-2bx0+c)x-2x03+bx02,
由于切线过原点,则-2x03+bx02=0,
解得x0=
,
∵若f(x)有三个不同的零点,分别为0,x2,x3,
则x2,x3是方程x2-bx+c=0的两个不同的根,由韦达定理得x2+x3=b,
即x0=
成立.
(ii)由(i)知,x2,x3是方程x2-bx+c=0的两个不同的根,
令g(x)=x2-bx+c,由x2,x3属于区间[0,2),
知g(x)的图象与x轴在(0,2)内有两个不同的交点,
则
,即
,
上述不等式组对应的点(b,c)形成的平面区域如图阴影部分表示:
又
=
=
,
令目标函数z=4c-b2,
则c=
+
,
于是问题转化为求抛物线c=
+
的图象如y轴截距的取值范围,
结合图象,截距分别在曲线段OM,N(2,0)处去上,下界,
则z∈(-4,0),
因此
∈(-1,0).

若f(x)在x=1处取得极值-1,
则
|
经检验知此时函数f(x)满足条件.
(Ⅱ)(i)证明:切线斜率k=f′(x0)=3x02-2bx0+c,
则切线方程为y-f(x0)=(3x02-2bx0+c)(x-x0),
化简得y=(3x02-2bx0+c)x-2x03+bx02,
由于切线过原点,则-2x03+bx02=0,
解得x0=
| b |
| 2 |
∵若f(x)有三个不同的零点,分别为0,x2,x3,
则x2,x3是方程x2-bx+c=0的两个不同的根,由韦达定理得x2+x3=b,
即x0=
| x2+x3 |
| 2 |
(ii)由(i)知,x2,x3是方程x2-bx+c=0的两个不同的根,
令g(x)=x2-bx+c,由x2,x3属于区间[0,2),
知g(x)的图象与x轴在(0,2)内有两个不同的交点,
则
|
|
上述不等式组对应的点(b,c)形成的平面区域如图阴影部分表示:
又
| f(x0) |
| x0 |
f(
| ||
|
| 4c-b2 |
| 4 |
令目标函数z=4c-b2,
则c=
| b2 |
| 4 |
| z |
| 4 |
于是问题转化为求抛物线c=
| b2 |
| 4 |
| z |
| 4 |
结合图象,截距分别在曲线段OM,N(2,0)处去上,下界,
则z∈(-4,0),
因此
| f(x0) |
| x0 |

点评:本题主要考查函数的零点,导数的几何意义,导数的应用线性规划邓基础知识,考查运算能力和推理论证能力,综合性较强,难度较大.

练习册系列答案
相关题目
二次函数f(x)=x2+bx+c在(m,m+1)内有两个不同的实根,则( )
A、f(m)和f(m+1)都大于
| ||
B、f(m)和f(m+1)至少有一个大于
| ||
C、f(m)和f(m+1)都小于
| ||
D、f(m)和f(m+1)至少有一个小于
|
执行如图的程序框图,那么输出的S=( )


| A、720 | B、120 |
| C、24 | D、-120 |
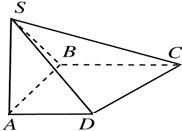 如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=
如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥底面ABCD,SA=AB=BC=1,AD=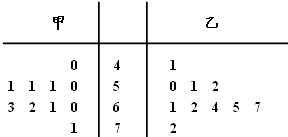 随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图:
随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图: