题目内容
f(x)=
在( )
| x |
| 1-x |
| A、(-∞,1)∪(1,+∞)上是增函数 |
| B、(-∞,1)∪(1,+∞)上是减函数 |
| C、(-∞,1),(1,+∞)分别是增函数 |
| D、(-∞,1),(1,+∞)分别是减函数 |
考点:函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:将f(x)变量分离得f(x)=-1-
,将y=
的图象向右平移1个单位,可得y=-
的图象,再向下平移1个单位,即可得到f(x)的图象,则有f(x)在x>1,x<1上均为增函数,即可得到结论.
| 1 |
| x-1 |
| -1 |
| x |
| 1 |
| x-1 |
解答:
解:f(x)=
=-
=-1-
,
由函数y=
在x>0,x<0均为增函数,
则将y=
的图象向右平移1个单位,可得y=-
的图象,
再向下平移1个单位,即可得到f(x)的图象,
则有f(x)在x>1,x<1上均为增函数,
则有函数f(x)的增区间为(-∞,1),(1,+∞).无减区间.
故选C.
| x |
| 1-x |
| x |
| x-1 |
=-1-
| 1 |
| x-1 |
由函数y=
| -1 |
| x |
则将y=
| -1 |
| x |
| 1 |
| x-1 |
再向下平移1个单位,即可得到f(x)的图象,
则有f(x)在x>1,x<1上均为增函数,
则有函数f(x)的增区间为(-∞,1),(1,+∞).无减区间.
故选C.
点评:本题考查函数的单调区间,考查图象的平移规律,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
若复数z满足(1-3i)z=10i,则z等于( )
| A、-1-3i | B、3-i |
| C、1+3i | D、-3+i |
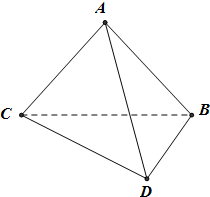 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.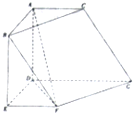 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.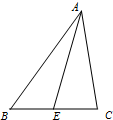 如图,在△ABC中,∠BAC=
如图,在△ABC中,∠BAC=