题目内容

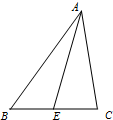如图，在△ABC中，∠BAC=
π
3
且BC=
3
．若E为BC的中点，则AE的最大值是
 
．
考点：正弦定理
专题：综合题,解三角形
分析：求出△ABC的外接圆的直径为
3
sin
π
3
=2，利用E为BC的中点，可得AE⊥BC时，AE取得最大值．
解答： 解：∵△ABC中，∠BAC=
π
3
且BC=
3
，
∴由正弦定理可得：△ABC的外接圆的直径为
3
sin
π
3
=2，
∵E为BC的中点，
∴AE⊥BC时，AE的最大值是1+
12-(
3
2
)2
=1+
1
2
=
3
2
．
故答案为：
3
2
．
点评：本题考查正弦定理的运用，考查学生分析解决问题的能力，求出△ABC的外接圆的直径是关键，属于中档题．
练习册系列答案
相关题目
已知集合A={x|x2-2x-3≤0，x∈R}，B={x|x2-2mx+m2-4≤0，x∈R}，若A∩B=[1，3]，求实数m的值．
已知函数f（x）=
1
2
ax2+2x+（2-a）lnx
（1）当a=-2时，求f（x）的最大值
（2）若在函数f（x）的定义域内存在区间D，使得该函数在区间D上为减函数，求a的取值范围
（3）若曲线C：y=f（x）在点x=1处的切线l与C有且只有一个公共点，求a的值．
f（x）=
x
1-x
在（　　）
A、（-∞，1）∪（1，+∞）上是增函数
B、（-∞，1）∪（1，+∞）上是减函数
C、（-∞，1），（1，+∞）分别是增函数
D、（-∞，1），（1，+∞）分别是减函数
设a，b为空间两条直线，α，β为空间两个平面，则下列命题中真命题的是（　　）
A、若a不平行α，则在α内不存在b，使得b平行a
B、若a不垂直α，则在α内不存在b，使得b垂直a
C、若α不平行β，则在β内不存在a，使得a平行α
D、若α不垂直β，则在β内不存在a，使得a垂直α
执行如图所示的程序框图输出的结果是（　　）
A、8B、6C、5D、3
执行如图的程序框图，输出的y等于（　　）
A、6B、7C、8D、9
（1）若α是第二象限角，sin（π-α）=
10
10
．求
2sin2
α
2
+8sin
α
2
cos
α
2
+8cos2
α
2
-5
2
sin(α-
π
4
)
 的值；
（2）已知函数f（x）=tan（2x+
π
4
），设α∈（0，
π
4
），若f（
α
2
）=2cos2α，求α的大小．
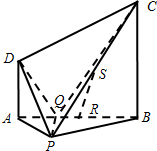已知四棱锥P-ABCD中，底面ABCD是直角梯形，平面PAB⊥平面ABCD，R、S分别是棱AB、PC的中点，AD∥BC，AD⊥AB，PA⊥PB，AB=BC=2AD=2PA=2，
（Ⅰ）求证：平面PAD⊥平面PBC；
（Ⅱ）求证：RS∥平面PAD
（Ⅲ）若点Q在线段AB上，且CD⊥平面PDQ，求三棱锥Q-PCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网