Question

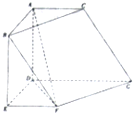在如图所示的几何体中，四边形ABED是矩形，四边形ADGC是梯形，AD⊥平面DEFG，EF∥DG，∠EDG=120°．
（Ⅰ）证明：FG⊥平面ADF；
（Ⅱ）求二面角A-CG-F的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（Ⅰ）取DG的中点M，连结FM，由已知得四边形DEFM是平行四边形，从而FG⊥DF，由此能证明FG⊥面ADF．
（Ⅱ）取EF的中点H，连结DH，以D为原点，DH为x轴，DG为y轴，DA为z轴，建立空间直角坐标系，利用向量法能求出二面角A-CG-F的余弦值．

解答： （Ⅰ）证明：取DG的中点M，连结FM，则EF=DM，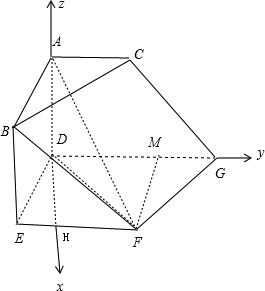
∵EF∥DG，∴四边形DEFM是平行四边形，
∴MF=DE=

1

2

DG=1，
∴△DFG是直角三角形，∴FG⊥DF，
又AD?平面ADF，DF?平面ADF，AD∩DF=D，
∴FG⊥面ADF．
（Ⅱ）解：取EF的中点H，连结DH，由（1）知DH⊥EF，
又EF∥DG，∴DH⊥DG，
又AD⊥平面DEFG，∴AD⊥DH，AD⊥DG，
以D为原点，DH为x轴，DG为y轴，DA为z轴，
建立空间直角坐标系，
则D（0，0，0），F（

3

2

，

1

2

，0），G（0，2，0），
C（0，1，1），

FG

=（-

3

2

，

3

2

，0），

GC

=（0，-1，1），
设平面FGC的法向量

n1

=（x，y，z），
则

n • FG =- 3 2 x+ 3 2 y=0 n • GC =-y+z=0

，取x=

3

，得

n

=（

3

，1，1），
又平面ACG的法向量

m

=（1，0，0），
∴cos＜

n

，

m

＞=

n • m

| n |•| m |

=

15

5

．
∴二面角A-CG-F的余弦值为

15

5

．

点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．