题目内容
已知递增的等比数列{an}前三项之积为8,且这三项分别加上1、2、2后又成等差数列.
(1)求等比数列{an}的通项公式;
(2)记bn=an+2n,求数列{bn}的前n项和Tn.
(1)求等比数列{an}的通项公式;
(2)记bn=an+2n,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用等差数列与等比数列的前n项和公式即可得出.
(2)利用等差数列与等比数列的前n项和公式即可得出.
解答:
解:(1)设等比数列前三项分别为a1,a2,a3,
则a1+1、a2+2、a3+2又成等差数列.依题意得:
,
即
,
解之得
,或
(数列{an}为递增等比数列,舍去),
∴数列{an}的通项公式:an=2n-1.
(2)由bn=an+2n得,bn=2n-1+2n,
∴Tn=b1+b2+…+bn=(20+2×1)+(21+2×2)+(22+2×3)+…+(2n-1+2n)
=(20+21+22+…+2n-1)+2(1+2+3+…+n)
=
+2×
=2n+n2+n-1.
则a1+1、a2+2、a3+2又成等差数列.依题意得:
|
即
|
解之得
|
|
∴数列{an}的通项公式:an=2n-1.
(2)由bn=an+2n得,bn=2n-1+2n,
∴Tn=b1+b2+…+bn=(20+2×1)+(21+2×2)+(22+2×3)+…+(2n-1+2n)
=(20+21+22+…+2n-1)+2(1+2+3+…+n)
=
| 20(1-2n) |
| 1-2 |
| n(1+n) |
| 2 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
f(x)=
在( )
| x |
| 1-x |
| A、(-∞,1)∪(1,+∞)上是增函数 |
| B、(-∞,1)∪(1,+∞)上是减函数 |
| C、(-∞,1),(1,+∞)分别是增函数 |
| D、(-∞,1),(1,+∞)分别是减函数 |
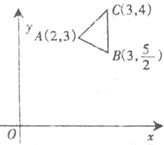 已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,
已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,| 5 |
| 2 |
A、a≥-
| ||
| B、a>0 | ||
C、a≤-
| ||
D、-
|
甲、乙、丙、丁四位同学站成一排照相留念,则甲、乙相邻的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
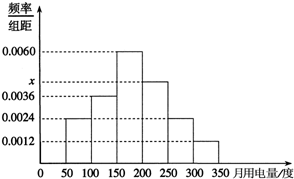
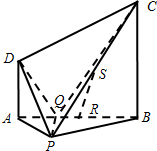 已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,
已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,