题目内容
过点M（1，3）作直线l，与抛物线y2=4x只有一个公共点，满足条件的直线有（ ）
| A、0条 | B、1条 | C、2条 | D、3条 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：根据点M（1，3）在抛物线y2=3x的外部，得到与抛物线C：y2=3x只有一个公共点的直线l有三条，有两条直线与抛物线相切，有一条直线与抛物线的对称轴平行，得到结果．
解答：
解：∵点M（1，3）在抛物线y2=4x的外部，
∴与抛物线C：y2=4x只有一个公共点的直线l有三条，分别是有两条直线与抛物线相切，有一条直线与抛物线的对称轴平行，
故选：D．
∴与抛物线C：y2=4x只有一个公共点的直线l有三条，分别是有两条直线与抛物线相切，有一条直线与抛物线的对称轴平行，
故选：D．
点评：本题考查直线与圆锥曲线的关系，本题解题的关键是忽略与对称轴平行的这条直线，容易得到有两条直线，本题是一个易错题．
练习册系列答案
相关题目
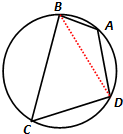已知圆内接四边形ABCD的边AB=1，BC=3，CD=DA=2．