题目内容
已知数列{an}是公差不为0的等差数列,a1=1,且a2,a4,a8成等比数列.
(1)求数列{an}的通项公式;
(2)若等比数列{bn}的各项都是正数,
=15,
=255,且在前n项和中,最大项为16,令Cn=an•bn,求数列{Cn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若等比数列{bn}的各项都是正数,
| Sn |
| 2 |
| S2n |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件得(1+3d)2=(1+d)(1+7d),解得d=1,或d=0(舍),由此求出an=1+(n-1)×1=n.
(2)设{bn}的公比为q,由已知条件得S2n=
=510,Sn=
30,两式相除,得1+qn=17,由在前n项和中,最大项为16,解得得b1=q=2,bn=2n.cn=an•bn=n•2n,由此利用错位相减法能求出数列{Cn}的前n项和Tn.
(2)设{bn}的公比为q,由已知条件得S2n=
| b1(1-q2n) |
| 1-q |
| b1(1-qn) |
| 1-q |
解答:
解:(1)∵数列{an}是公差不为0的等差数列,a1=1,且a2,a4,a8成等比数列,
∴(1+3d)2=(1+d)(1+7d),
解得d=1,或d=0(舍),
∴an=1+(n-1)×1=n.
(2)设{bn}的公比为q,
∵
=15,
=255,
∴S2n=
=510,Sn=
30,
两式相除,得1+qn=17,
∴bn=b1qn-1=
•qn16•
,
∵在前n项和中,最大项为16,
∴只有
=1时最大,故b1=q时取得.
将所得结果代入到
=15,求得b1=q=2,bn=2n.
cn=an•bn=n•2n,
Tn=1•2+2•22+3•23+…+n•2n,①
2Tn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得-Tn=2+22+23+…+2n-n•2n+1
=2n+1-2-n•2n+1
=-(n-1)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
∴(1+3d)2=(1+d)(1+7d),
解得d=1,或d=0(舍),
∴an=1+(n-1)×1=n.
(2)设{bn}的公比为q,
∵
| Sn |
| 2 |
| S2n |
| 2 |
∴S2n=
| b1(1-q2n) |
| 1-q |
| b1(1-qn) |
| 1-q |
两式相除,得1+qn=17,
∴bn=b1qn-1=
| b1 |
| q |
| b1 |
| q |
∵在前n项和中,最大项为16,
∴只有
| b1 |
| q |
将所得结果代入到
| Sn |
| 2 |
cn=an•bn=n•2n,
Tn=1•2+2•22+3•23+…+n•2n,①
2Tn=1•22+2•23+3•24+…+n•2n+1,②
①-②,得-Tn=2+22+23+…+2n-n•2n+1
=2n+1-2-n•2n+1
=-(n-1)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a,b∈R,且ab>0,则下列不等式中,恒成立的是( )
| A、a2+b2>2ab | ||
B、a+b≥2
| ||
C、a+b>2
| ||
| D、a2+b2≥2ab |
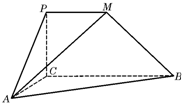 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.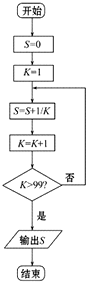 给出一个算法的程序框图(如图所示).
给出一个算法的程序框图(如图所示).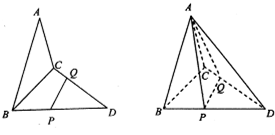 如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.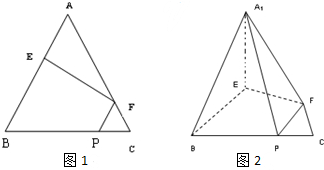
 如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=
如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=