题目内容
在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足
=
=
=
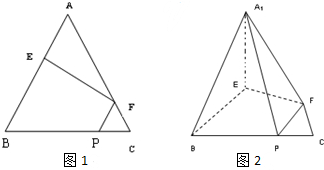
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B,A1P(如图).
(I)求证:A1E⊥平面BEP;
(Ⅱ)求点B到面A1PF的距离;
(Ⅲ)求异面直线BP与A1F所成角的余弦.
| AE |
| EB |
| CF |
| FA |
| CP |
| PB |
| 1 |
| 2 |
(I)求证:A1E⊥平面BEP;
(Ⅱ)求点B到面A1PF的距离;
(Ⅲ)求异面直线BP与A1F所成角的余弦.

考点:异面直线及其所成的角,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(I)利用面面垂直的性质定理判断;
(Ⅱ)点B到面A1PF的距离进行转化,B到面面A1PF的距离即为E到面面A1PF的距离,E到面A1PF的距离即为△A1EF中E到A1F的距离;
(Ⅲ)DF∥BP∴∠DFA1即为所求角
(Ⅱ)点B到面A1PF的距离进行转化,B到面面A1PF的距离即为E到面面A1PF的距离,E到面A1PF的距离即为△A1EF中E到A1F的距离;
(Ⅲ)DF∥BP∴∠DFA1即为所求角
解答:
(本小题满分12分)证明:(I)在图1中,取BE的中点D,连DF
∵
=
=
=
,∵AF=AD=2,又∠A=60°∴△ADF为正三角形
又∵AE=ED=1∴EF⊥AD∴在图2中有A1E⊥EF,BE=EF
∴∠A1EB为二面角A1-EF-B的平面角∵二面角A1-EF-B为直二面角∴A1E⊥BE
又∵BE∩EF=E,∴A1E⊥面BEF,即A1E⊥面BEP-----------(4分)
(Ⅱ)∵BE∥PF∴BE∥面A1PF,∵B到面面A1PF的距离即为E到面面A1PF的距离,
∵BE⊥面A1EF,又BE∥PF,∴PF⊥面A1EF
∴面A1EF⊥面A1PF∵E到面A1PF的距离即为△A1EF中E到A1F的距离
d=A1E×sin60°=
∴点B到面A1PF的距离为
-------------(8分)
(Ⅲ)∵DF∥BP∴∠DFA1即为所求角
△A1DF中A1D=
,DF=2,A1F=2,cos∠DFA1=
=
∴异面直线BP与A1F所成角的余弦值为
-----------(12分)
∵
| AE |
| EB |
| CF |
| FA |
| CP |
| PB |
| 1 |
| 2 |
又∵AE=ED=1∴EF⊥AD∴在图2中有A1E⊥EF,BE=EF
∴∠A1EB为二面角A1-EF-B的平面角∵二面角A1-EF-B为直二面角∴A1E⊥BE
又∵BE∩EF=E,∴A1E⊥面BEF,即A1E⊥面BEP-----------(4分)
(Ⅱ)∵BE∥PF∴BE∥面A1PF,∵B到面面A1PF的距离即为E到面面A1PF的距离,
∵BE⊥面A1EF,又BE∥PF,∴PF⊥面A1EF
∴面A1EF⊥面A1PF∵E到面A1PF的距离即为△A1EF中E到A1F的距离
d=A1E×sin60°=
| ||
| 2 |
| ||
| 2 |
(Ⅲ)∵DF∥BP∴∠DFA1即为所求角
△A1DF中A1D=
| 2 |
| DF2+A1F2+A1D2 |
| 2DF•A1F |
| 3 |
| 4 |
∴异面直线BP与A1F所成角的余弦值为
| 3 |
| 4 |
点评:本题考查直线与平面垂直的证明,考查点面距,考查异面直线所成角的余弦值的求法,解题时要认真审题,注意问题的转化.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
在下列命题中,真命题是( )
A、“抛物线y=-x2+1与x轴围成的封闭图形面积为
| ||||
| B、“若抛物线的方程为y2=4x,则其焦点到其准线的距离为2”的逆命题 | ||||
C、“若向量
| ||||
| D、“若|x-1|+|x+2|=3,则-1≤x≤2”的逆否命题 |