题目内容
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设Cn=
,求数列{Cn}的前n项和Tn.
(1)求数列{an}和{bn}的通项公式;
(2)设Cn=
| 2 |
| an(4-log2bn) |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用公式当n≥2时,an=sn-sn-1,即可求得通项公式;
(2)利用裂项相消法即可得出数列的和.
(2)利用裂项相消法即可得出数列的和.
解答:
解:(1)设等比数列{bn}的公比为q,
当n≥2时,an=sn-sn-1=2n2-2(n-1)2=4n-2;
当n=1时,a1=2,符号上式;
所以,an=4n-2,
又b1=a1=2,a2=6,所以,b2=
=
,
于是,q=
=
=
,
所以,bn=2×(
)n-1=23-2n.
(2)由(1)得,Cn=
=
=
(
-
),
所以Tn=
(1-
+
-
+…+
-
)=
(1-
)=
.
当n≥2时,an=sn-sn-1=2n2-2(n-1)2=4n-2;
当n=1时,a1=2,符号上式;
所以,an=4n-2,
又b1=a1=2,a2=6,所以,b2=
| b1 |
| a2-a1 |
| 1 |
| 2 |
于是,q=
| b2 |
| b1 |
| ||
| 2 |
| 1 |
| 4 |
所以,bn=2×(
| 1 |
| 4 |
(2)由(1)得,Cn=
| 2 |
| an(4-log2bn) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题主要考查学生数列的通项公式及数列求和的方法的运用能力,考查学生的运算求解能力,属中档题.

练习册系列答案
相关题目
设△ABC的三个内角A,B,C所对的边分别是a,b,c,已知A=60°,a=
,c=
,则b=( )
| 6 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
已知tan(π-a)=2,则
=( )
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=2x+2-x |
| C、f(x)=lg(1+x)-lg(1-x) |
| D、f(x)=x3-1 |
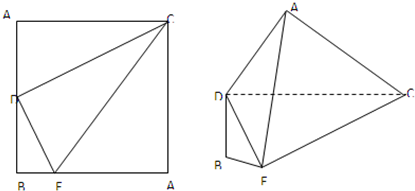 如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.
如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.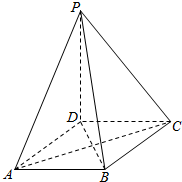 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.