题目内容
已知tan(π-a)=2,则
=( )
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式左边利用诱导公式化简求出tanα的值,原式利用同角三角函数间基本关系弦化切后将tanα的值代入计算即可求出值.
解答:
解:∵tan(π-a)=-tanα=2,
∴tanα=-2,
则原式=
=
=
=-
.
故选:C.
∴tanα=-2,
则原式=
| sin2α+cos2α |
| sinαcosα |
| tan2α+1 |
| tanα |
| 4+1 |
| -2 |
| 5 |
| 2 |
故选:C.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
“mn<0”是方程mx2+ny2=1表示双曲线的( )条件.
| A、充分不必要 | B、必要不充分 |
| C、充要 | D、不充分不必要 |
已知向量
=(2,-4),
=(3,4)则向量
在
方向上的投影为( )
| a |
| b |
| a |
| b |
A、
| ||||
B、-
| ||||
| C、2 | ||||
| D、-2 |
等差数列{an}共有20项,其中奇数项的和为15,偶数项的和为45,则该数列的公差为( )
| A、-3 | B、3 | C、-2 | D、-1 |
已知x∈(0,
),则y=x
的最大值为( )
| 1 |
| 4 |
| 1-4x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设f(x)=ax+a+4,若f′(1)=2,则a等于( )
| A、1 | B、-2 | C、2 | D、-3 |
已知椭圆
+
=1,则以点M(-1,1)为中点的弦所在直线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、3x-4y+7=0 |
| B、3x+4y-1=0 |
| C、4x-3y+7=0 |
| D、4x+3y+1=0 |
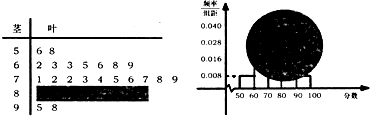 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题: