题目内容
已知数列{an}的前n项和为Sn,a1=2,nan+1=Sn+n(n+1),bn=an•2n-1,则{bn}的前n项和Tn= .
考点:数列递推式
专题:综合题,等差数列与等比数列
分析:由nan+1=Sn+n结合通项和前n项和的关系,转化为an+1-an=2(n≥2)再由等差数列的定义求解an代入整理得{bn}是一个等差数列与等比数列对应项积的形式,用错位相减法求其前n项和.
解答:
解:∵nan+1=Sn+n(n+1),(n-1)an=Sn-1+n(n-1),
∴nan+1-(n-1)an=an+2n,
∴an+1-an=2(n≥2),
a1=2,a2=S1+2,
∴a2-a1=2,
∴{an}等差数列,
∴an=2n
∴bn=an•2n-1=2n•2n-1=n•2n,
∴Tn=2+2•22+…+n•2n,
∴2Tn=2•22+…+(n-1)•2n+n•2n+1,
两式相减可得Tn=2+(n-1)•2n+1.
故答案为:Tn=2+(n-1)•2n+1.
∴nan+1-(n-1)an=an+2n,
∴an+1-an=2(n≥2),
a1=2,a2=S1+2,
∴a2-a1=2,
∴{an}等差数列,
∴an=2n
∴bn=an•2n-1=2n•2n-1=n•2n,
∴Tn=2+2•22+…+n•2n,
∴2Tn=2•22+…+(n-1)•2n+n•2n+1,
两式相减可得Tn=2+(n-1)•2n+1.
故答案为:Tn=2+(n-1)•2n+1.
点评:本题主要考查数列的转化与通项公式和求和方法,这里涉及了通项与前n项和之间的关系及错位相减法,这是数列考查中常考常新的问题,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将四个数a=
,b=
,c=
,d=
从小到大排列是( )
| 3 | 2 |
| 3 | -2 |
| 1 | |||
|
| 3 | 4 |
| A、b<a<c<d |
| B、b<c<d<a |
| C、b<c<a<d |
| D、a<b<c<d |
不等式2x-x2>0的解集为( )
| A、(-∞,2) |
| B、(-∞,0)∪(2,+∞) |
| C、(2,+∞) |
| D、(0,2) |
函数f(x)=1-
(a>0,a≠1)是定义在R上的奇函数,当x∈(0,1]时,tf(x)≥2x-2恒成立,则实数t的取值范围是( )
| 4 |
| 2ax+a |
| A、[0,+∞) |
| B、[2,+∞) |
| C、[4,+∞) |
| D、(-2,+∞) |
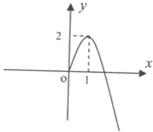 已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.
已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.