题目内容
3.已知函数f(x)=$\frac{a}{3}{x^3}+\frac{b}{2}{x^2}-{a^2}$x(a>0,b∈R).(Ⅰ)当a=1时,判断函数f(x)在R上的单调性,并证明你的结论;
(Ⅱ)若x1,x2是函数f(x)的两个不同的极值点,且|x1-x2|=$\sqrt{\frac{2}{a}-1}$,求实数a,b的取值范围.
分析 (Ⅰ)求出函数的导数,得到f′(x)>0,求出函数的单调区间即可;
(Ⅱ)求出函数的导数,求出${x_1}+{x_2}=-\frac{b}{a},{x_1}{x_2}=-a$,代入|x1-x2|=$\sqrt{\frac{2}{a}-1}$,得到关于a的不等式,求出a的范围,得到${b^2}=g(a)=-4{a^3}-{a^2}+2a({0<a<\frac{{\sqrt{33}-1}}{8}})$,根据函数的单调性求出b的范围即可.
解答 解:(Ⅰ)当a=1时,$f(x)=\frac{1}{3}{x^3}+\frac{b}{2}{x^2}-x$,则f'(x)=x2+bx-1
而方程x2+bx-1=0的判别式△=b2+4>0恒成立,
所以f'(x)=x2+bx-1>0恒成立,即函数f(x)在R上的单调递增.
(II)∵$f(x)=\frac{a}{3}{x^3}+\frac{b}{2}{x^2}-{a^2}x$,
∴f'(x)=ax2+bx-a2.x1,x2是函数f(x)的两个不同的极值点,
则x1,x2是方程ax2+bx-a2=0的两个不同的实数根,
即${x_1}+{x_2}=-\frac{b}{a},{x_1}{x_2}=-a$,且△=b2-4a(-a2)=b2+4a3>0
∵$|{x_1}-{x_2}|=\sqrt{\frac{2}{a}-1}({0<a≤2})$,即$|{x_1}-{x_2}{|^2}=\frac{2}{a}-1⇒{({{x_1}+{x_2}})^2}-4{x_1}{x_2}=\frac{2}{a}-1$,
∴${({-\frac{b}{a}})^2}+4a=\frac{2}{a}-1$,即b2+4a3=2a-a2,则$\left\{\begin{array}{l}-4{a^3}-{a^2}+2a≥0\\ 2a-{a^2}>0\end{array}\right.$
即$\left\{\begin{array}{l}4{a^2}+a-2≤0\\ 0<a<2\end{array}\right.⇒0<a≤\frac{{\sqrt{33}-1}}{8}$(10分)
又${b^2}=g(a)=-4{a^3}-{a^2}+2a({0<a<\frac{{\sqrt{33}-1}}{8}})$,
$g'(a)=-12{a^2}-2a+2=0⇒a=\frac{1}{3},a=-\frac{1}{2}$(舍)
当$0<a<\frac{1}{3}$时,g'(a)>0,函数g(a)是增函数;
当$\frac{1}{3}<a<\frac{{\sqrt{33}-1}}{8}$时,g'(a)<0,函数g(a)是减函数;
当$a=\frac{1}{3}$时,函数g(a)取到最大值$g({\frac{1}{3}})=\frac{11}{27}$
所以$0<{b^2}≤\frac{11}{27}⇒b∈[{-\frac{{\sqrt{33}}}{9},0})∪({0,\frac{{\sqrt{33}}}{9}}]$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

| A. | -$\frac{13}{5}$+$\frac{1}{5}$i | B. | -$\frac{13}{5}$-$\frac{1}{5}$i | C. | $\frac{13}{5}$+$\frac{1}{5}$i | D. | $\frac{13}{5}$-$\frac{1}{5}$i |
| A. | 6 | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{15}$ |
| A. | $(-∞,\frac{e}{3})$ | B. | $(\frac{e}{3},{e^2})$ | C. | $(\frac{e}{3},\frac{e^2}{6})$ | D. | $(\frac{e}{3},+∞)$ |
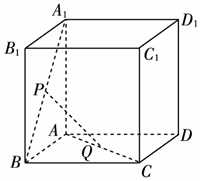 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.